3 Vectors in General; \(\mathbb{R}^n\) and \(\mathbb{C}^n\)
3.1 Vectors in \(\mathbb{R}^n\)
3.1.1 Definitions
If we regard vectors as sets of components, it is easy to generalise from 3 to \(n\) dimensions.
Definition 3.1 \(\mathbb{R}^n = \{ \underline{x} = (x_1, x_2, \dots, x_n) : x_i \in \mathbb{R} \}\)
Definition 3.2
addition \(\underline{x} + \underline{y} = (x_1 + y_1, \dots, x_n + y_n)\) for any \(\underline{x}, \underline{y} \in \mathbb{R}^n\)
scalar multiplication \(\lambda x = (\lambda x_1, \dots, \lambda x_n)\) for any \(\underline{x} \in \mathbb{R}^n\) and \(\lambda \in \mathbb{R}\)
Definition 3.3 (Inner/ scalar product) \(\underline{x} \cdot \underline{y} = \sum_i x_i y_i = x_1 y_1 + \dots + x_n y_n\)
Symmetric \(\underline{x} \cdot \underline{y} = \underline{y} \cdot \underline{x}\)
Bilinear (linear in each vector) \[\begin{align*} (\lambda \underline{x} + \lambda' \underline{x}') \cdot \underline{y} &= \lambda (\underline{x} \cdot \underline{y}) + \lambda' (\underline{x}' \cdot \underline{y}) \\ \underline{x} \cdot (\mu \underline{y} + \mu' \underline{y}') &= \mu (\underline{x} \cdot \underline{y}) + \mu' (\underline{x} \cdot \underline{y}) % (\lambda \underline{y} + \lambda' \underline{y}) \cdot \underline{x} &= \lambda (\underline{y} \cdot \underline{x}) + \lambda' (\underline{y}' \cdot \underline{x}) \end{align*}\]
Positive definite \(\underline{x} \cdot \underline{x} = \sum_i x^2_i \geq 0\) and \(= 0 \iff \underline{x} = \underline{0}\). The length or norm of vector \(\underline{x}\) is \(| \underline{x} | \geq 0\) defined by \(| \underline{x} |^2 = \underline{x} \cdot \underline{x}\).
For \(\underline{x} \in \mathbb{R}^n\) we can write \(\underline{x} = \sum_i x_i \underline{e}_i\) where \[\begin{align*} \underline{e}_1 &= (1, 0, \dots, 0) \\ \underline{e}_2 &= (0, 1, \dots, 0) \\ &\;\;\vdots \\ \underline{e}_n &= (0, 0, \dots, 1). \end{align*}\] We call \(\{ \underline{e}_i \}\) the standard basis for \(\mathbb{R}^n\). Note it is orthonormal: \[\begin{align*} \underline{e}_i \cdot \underline{e}_j = \delta_{ij} = \begin{cases} 1 & \text{ if } i = j \\ 0 & \text{ if } i \neq j \end{cases} \end{align*}\]
3.1.2 Cauchy-Schwarz and Triangle Inequalities
Proposition 3.1 (Cauchy-Schwarz) \(|\underline{x} \cdot \underline{y}| \leq |\underline{x}| | \underline{y}|\) for some \(\underline{x}, \underline{y} \in \mathbb{R}^n\) and equality holds iff \(\underline{x} = \lambda \underline{y}\) or \(\underline{y} = \lambda \underline{x}\) \((\underline{x} \parallel \underline{y})\) for some \(\lambda \in \mathbb{R}\).
Deductions reveal geometrical aspects of the inner product:
Set \(\underline{x} \cdot \underline{y} = |\underline{x}| |\underline{y}| \cos \theta\) to define angle \(\theta\) between \(\underline{x}\) and \(\underline{y}\)
Triangle inequality holds \(| \underline{x} + \underline{y} | \leq |\underline{x}| + |\underline{y}|\).
Proof (Cauchy-Schwarz). If \(\underline{y} = 0\), the result is immediate. If \(\underline{y} \neq 0\), consider \[\begin{align*} |\underline{x} - \lambda \underline{y}|^2 &= (\underline{x} - \lambda \underline{y}) \cdot (\underline{x} - \lambda \underline{y}) \\ &= |\underline{x}|^2 - 2 \lambda \underline{x} \cdot \underline{y} + \lambda^2 | \underline{y} | \geq 0 \end{align*}\] This is a quadratic in \(\lambda \in \mathbb{R}\) with at most one real root, so discriminant satisfies \((-2 \underline{x} \cdot \underline{y})^2 - 4 |\underline{x}|^2 |\underline{y}|^2 \leq 0\) as required. Equality holds iff discriminant \(= 0\) iff \(\lambda \underline{y} = \underline{x}\) for some \(\lambda \in \mathbb{R}\).
Proof (Triangle inequality). \[\begin{align*} LHS^2 &= |\underline{x} + \underline{y}|^2 = |\underline{x}|^2 + 2 \underline{x} \cdot \underline{y} + |\underline{y}|^2 \\ RHS^2 &= (|\underline{x}| + |\underline{y}|)^2 = |\underline{x}|^2 + 2 |\underline{x}| |\underline{y}| + |\underline{y}|^2 \end{align*}\] and compare using Cauchy-Schwarz.
3.2 Vector Spaces
3.2.1 Axioms; span; subspaces
Let \(V\) be a set of objects called vectors with operations
\[\begin{align*} \left.\begin{aligned} &i. & \underline{v} + \underline{w} &\in V \\ &ii. & \lambda \underline{v} &\in V \end{aligned}\right\} \text{defined } \forall \; v, w \in V, \text{ and } \forall \; \lambda \in \mathbb{R}. \end{align*}\] Then \(V\) is a real vector space if \(V\) is an abelian group under addition and \[\begin{align*} \lambda ( \underline{v} + \underline{w}) &= \lambda \underline{v} + \lambda \underline{w} \\ (\lambda + \mu) \underline{v} &= \lambda \underline{v} + \mu \underline{v} \\ \lambda (\mu \underline{v}) &= (\lambda \mu) \underline{v} \\ 1 \underline{v} &= \underline{v} \end{align*}\]3 (the first three are same as Vector Addition and Scalar Multiplication)
These axioms or key properties apply to geometrical vectors with \(V\) being a 3d space or to vectors in \(V = \mathbb{R}^n\), as above, as well as other examples.
For vectors \(\underline{v}_1, \underline{v}_2, \dots, \underline{v}_r \in V\) we can form a linear combination \(\lambda_1 \underline{v}_1 + \lambda_2 \underline{v}_2 + \dots + \lambda_r \underline{v}_r \in V\) for any \(\lambda_i \in \mathbb{R}\); the span is defined \(\operatorname{span} \{ \underline{v}_1, \underline{v}_2, \dots, \underline{v}_r \} = \{ \sum_i \lambda_i \underline{v}_i : \lambda_i \in \mathbb{R} \}\).
A subspace of \(V\) is a subset that is itself a vector space.
Note \(V\) and \(\{ 0 \}\) are subspaces.
\(\operatorname{span} \{ \underline{v}_1, \underline{v}_2, \dots, \underline{v}_r \}\) is a subspace for any vectors \(\underline{v}_1, \underline{v}_2, \dots, \underline{v}_r\).
Note: a non-empty subset \(U \subseteq V\) is a subspace iff
\[\begin{align*}
\underline{v}, \underline{w} \in U \implies \lambda \underline{v} + \mu \underline{w} \in U \quad \forall \; \lambda, \mu \in \mathbb{R}.
\end{align*}\]
Example 3.1 In \(\mathbb{R}^3\), a line or plane through \(\underline{0}\) is a subspace but if it doesn’t contain \(\underline{0}\) it is not a subspace. e.g. \[\begin{gather} \underline{v}_1 = \begin{pmatrix}1 \\0 \\-1\end{pmatrix}, \underline{v}_2 = \begin{pmatrix}1 \\1 \\-2\end{pmatrix}, \underline{n} = \begin{pmatrix}1 \\1 \\1\end{pmatrix} \\ \operatorname{span} \{ \underline{v}_1, \underline{v}_2\} = \{ \underline{r} : \underline{n} \cdot \underline{r} = 0 \} \text{ this is a plane and subspace} \\ \text{But } \{ \underline{r} : \underline{n} \cdot \underline{r} = 1 \} \text{ this is a plane but not a subspace } [\underline{r}, \underline{r}' \text{ on plane then } (\underline{r} + \underline{r}') \cdot \underline{n} = 2] \end{gather}\]
3.2.2 Linear Dependence and Independence
For vectors \(\underline{v}_1, \underline{v}_2, \dots, \underline{v}_r \in V\) (where \(V\) is a real vector space) consider the linear relation \[\begin{align*} \lambda_1 \underline{v}_1 + \lambda_2 \underline{v}_2 + \dots + \lambda_r \underline{v}_r = \underline{0} \tag{3.1} \end{align*}\]
If (3.1) \(\implies \lambda_i = 0\) for every \(i\) then the vectors form a linearly independent set (they obey only the trivial linear relation with \(\lambda_i = 0\)).
If (3.1) holds with at least one \(\lambda_i \neq 0\) then the vectors form a linearly dependent set (they obey a non-trivial linear relation).
Example 3.2 \[\begin{gather} \left\{ \begin{pmatrix}1 \\0\end{pmatrix}, \begin{pmatrix}0 \\1\end{pmatrix}, \begin{pmatrix}0 \\2\end{pmatrix} \right\} \text{ are linearly dependent because:} \\ 0 \begin{pmatrix}1 \\0\end{pmatrix} + 2 \begin{pmatrix}0 \\1\end{pmatrix} + (-1) \begin{pmatrix}0 \\2\end{pmatrix} = \underline{0} \end{gather}\] Note we cannot express \(\begin{pmatrix}1 \\0\end{pmatrix}\) in terms of the others.
Example 3.3 Any set containing \(\underline{0}\) is linearly dependent.
e.g. \[\begin{align*}
\left\{ \begin{pmatrix}1 \\0\end{pmatrix}, \begin{pmatrix}0 \\0\end{pmatrix}\right\} \text{ have} \\
0 \begin{pmatrix}1 \\0\end{pmatrix} + 412 \begin{pmatrix}0 \\0\end{pmatrix}= \underline{0}
\end{align*}\] which is a non-trivial linear relation.
Example 3.4 \(\left\{ \underline{a}, \underline{b}, \underline{c} \right\}\) in \(\mathbb{R}^3\) are linearly independent if \(\underline{a} \cdot \underline{b} \wedge \underline{c} \neq 0\). Consider \(\alpha \underline{a} + \beta \underline{b} + \gamma \underline{c} = \underline{0}\). Take dot with \(\underline{b} \wedge \underline{c}\) to get \(\alpha \underline{a} \cdot \underline{b} \wedge \underline{c} = 0 \implies \alpha = 0\) and \(\beta = \gamma = 0\) similarly.
3.2.3 Inner product
This is an additional structure on a real vector space \(V\), also characterised by axioms. For \(\underline{v}, \underline{w} \in V\) write inner product \(\underline{v} \cdot \underline{w}\) or \((\underline{v}, \underline{w}) \in \mathbb{R}\). This satisfies axioms corresponding to the properties in Definitions
Symmetric
Bilinear
Positive definite
Lemma 3.1 In a real vector space \(V\) with inner product, if \(\underline{v}_1, \dots, \underline{v}_r\) are non-zero and orthogonal: \[\begin{align*} (\underline{v}_i, \underline{v}_i) \neq 0 \text { and } (\underline{v}_i, \underline{v}_j) = 0 \text{ where } i \neq j \text{ and for fixed } i. \end{align*}\] then \(\underline{v}_1, \dots, \underline{v}_r\) are linearly independent.
Proof. \[\begin{align*} \text{Consider } \sum_i \alpha_i \underline{v}_i &= \underline{0} \\ (\underline{v}_j, \sum_i \alpha_i \underline{v}_i) &= \sum_i \alpha_i (\underline{v}_j, \underline{v}_i) \\ 0 &= \alpha_j (\underline{v}_j, \underline{v}_j) \text{ all fixed j} \\ \implies \alpha_j &= 0. \end{align*}\]
3.3 Bases and Dimension
For a vector space \(V\), a basis is a set \[\begin{align*} \mathcal{B} = \{ \underline{e}_1, \dots, \underline{e}_n \} \end{align*}\] such that
\(\mathcal{B}\) spans \(V\), i.e. any \(\underline{v} \in V\) can be written \(\underline{v} = \sum_{i=1}^{n} v_i \underline{e_i}\)
\(\mathcal{B}\) is linearly independent.
Given ii., the coefficients \(v_i\) in i. are unique since \[\begin{align*} \sum_i v_i \underline{e}_i &= \sum v_i' \underline{e}_i \\ \implies \sum_i (v_i - v_i') \underline{e}_i &= \underline{0} \\ \implies v_i &= v_i' \end{align*}\]
\(v_i\) are components of \(\underline{v}\) w.r.t. \(\mathcal{B}\)
Example 3.5 Standard basis for \(\mathbb{R}^n\) consisting of \[\begin{align*} \underline{e}_1 &= (1, 0, \dots, 0) \\ \underline{e}_2 &= (0, 1, \dots, 0) \\ &\;\;\vdots \\ \underline{e}_n &= (0, 0, \dots, 1). \end{align*}\] is a basis according to general definition.
\[\begin{align*} \underline{x} = \begin{pmatrix}x_1 \\\vdots \\x_n\end{pmatrix} = x_1 \underline{e}_1 + \dots + x_n \underline{e}_n \end{align*}\]
\(\underline{x} = \underline{0} \iff x_1 = x_2 = \dots = x_n = 0\)
Many other bases can be chosen
Example 3.6 In \(\mathbb{R}^2\) we have bases \[\begin{align*} \left\{ \begin{pmatrix}0 \\1\end{pmatrix}, \begin{pmatrix}1 \\1\end{pmatrix} \right\} \text{ or } \left\{ \begin{pmatrix}1 \\1\end{pmatrix}, \begin{pmatrix}1 \\ -1\end{pmatrix} \right\} \end{align*}\] or \(\{ \underline{a}, \underline{b} \}\) for any \(\underline{a}, \underline{b} \in \mathbb{R}^2\) with \(\underline{a} \nparallel \underline{b}\).
Example 3.7 In \(\mathbb{R}^3, \{ \underline{a}, \underline{b}, \underline{c} \}\) is a basis iff \(\underline{a} \cdot \underline{b} \wedge \underline{c} \neq 0\).
Consider previous example of plane through \(\underline{0}\), subspace in \(\mathbb{R}^3\)
\[\begin{align*}
\underline{n} \cdot \underline{r} = 0 \text{ with } \underline{n} = \begin{pmatrix}1 \\1 \\1\end{pmatrix}
\end{align*}\]
we have \[\begin{align*}
\{ \underline{v}_1, \underline{v}_2 \} \text{ basis with } \underline{v}_1 = \begin{pmatrix}1 \\0 \\-1\end{pmatrix}, \underline{v}_2 = \begin{pmatrix}1 \\1 \\-2\end{pmatrix}
\end{align*}\]
not normalised or orthogonal.
But we could choose orthonormal basis
\[\begin{align*}
\{ \underline{u}_1, \underline{u}_2 \} \text{ with } \underline{u}_1 = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\-1 \\ 0 \end{pmatrix} \text{ and } \underline{u}_2 = \frac{1}{\sqrt{6}} \begin{pmatrix} 1 \\1 \\ -2 \end{pmatrix}.
\end{align*}\]
Theorem 3.1 If \(\{ \underline{e}_1, \dots, \underline{e}_n \}\) and \(\{ \underline{f}_1, \dots, \underline{f}_m \}\) are bases for a real vector space \(V\), then \(n = m\).
Definition 3.4 The number of vectors in any basis is the dimension of \(V\), \(\dim V\).
Note: \(\mathbb{R}^n\) has dimension \(n\).
Proof. \[\begin{align*} \underline{f}_a &= \sum_i A_{ai} \underline{e}_i \\ \text{and } \underline{e}_i &= \sum_i B_{ia} \underline{f}_a \end{align*}\] for constants \(A_{ai}\) and \(B_{ia}\) and we use ranges of indices \(i, j = 1, \dots, n\) and \(a, b = 1, \dots, m\).4 \[\begin{align*} \implies \underline{f}_a &= \sum_i A_{ai} \left( \sum_b B_{ib} \underline{f}_b \right) \\ &= \sum_b \left( \sum_i A_{ai} B_{ib} \right) \underline{f}_b. \end{align*}\] But coeffs w.r.t a basis are unique so \(\sum_i A_{ai} B_{ib} = \delta_{ab}\).
Similarly, \[\begin{align*} \underline{e}_i &= \sum_j \left( \sum_a B_{ia} A_{aj} \right) \underline{e}_j \end{align*}\] and hence \[\begin{align*} \sum_a B_{ia} A_{aj} = \delta_{ij}. \end{align*}\] Now \[\begin{align*} \sum_{i, a} A_{ai} B_{ia} &= \sum_a \delta_{aa} = m \\ &= \sum_{i, a} B_{ia} A_{ai} = \sum_i \delta_{ii} = n \\ \implies m &= n \end{align*}\]
Note: by convention the vector space \(\{ 0 \}\) has dimension \(0\).
Not every vector space is finite dimensional.
Proposition 3.2 Let \(V\) be a vector space of dimension \(n\)
If \(Y = \{ \underline{w}_1, \dots, \underline{w}_m \}\) spans V, then \(m \geq n\) and if \(m > n\) vectors can be removed from \(Y\) to get a basis.
If \(X = \{ \underline{u}_1, \dots, \underline{u}_k \}\) are linearly independent then \(k \leq n\) and if \(k < n\) vectors can be added to \(X\) to get a basis.
3.4 Vectors in \(\mathbb{C}^n\)
3.4.1 Definitions
Definition 3.5 \(\mathbb{C}^n = \{ \underline{z} = (z_1, \dots, z_n) : z_j \in \mathbb{C} \}\)
Definition 3.6 addition: \(\underline{z} + \underline{w} = \left( z_1 + w_1, \dots, z_n + w_n \right)\)
scalar multiplication: \(\lambda \underline{z} = (\lambda z_1, \dots, \lambda z_n)\) for any \(\underline{z}, \underline{w} \in \mathbb{C}^n\).
Taking real scalars \(\lambda, \mu \in \mathbb{R}\), \(\mathbb{C}^n\) is a real vector space obeying axioms or key properties in Axioms; span; subspaces.
Taking complex scalars \(\lambda, \mu \in \mathbb{C}\), \(\mathbb{C}^n\) is a complex vector space - same axioms/ key properties hold, and definitions of linear combinations, linear (in)dependence, span, bases, dimension all generalise to complex scalars.
The distinction matters
\[\begin{align*}
e.g. \ \underline{z} &= (z_1, \dots, z_n) \in \mathbb{C}^n \\
\text{with } z_j &= x_j + i y_j \hspace{0.5cm} x_j, y_j \in \mathbb{R} \\
\text{then } \underline{z} &= \sum_j x_j \underline{e}_j + \sum_j y_j \underline{f}_j \text{ is a real linear combination} \\
\text{where } \underline{e}_j &= \begin{pmatrix}0 & \dots & 1 & \dots & 0\end{pmatrix} \\
\underline{f}_j &= \begin{pmatrix}0 & \dots & i & \dots & 0\end{pmatrix}
\end{align*}\]
\(\therefore \{\underline{e}_1, \dots, \underline{e}_n, \underline{f}_1, \dots, \underline{f}_n \}\) is a basis for \(\mathbb{C}^n\) as a real vector space.
So the real dimension is \(2n\).
But \(\underline{z} = \sum_j z_j \underline{e}_j\) and \(\{ \underline{e}_1, \dots, \underline{e}_n \}\) is a basis for \(\mathbb{C}^n\) as a complex vector space, dimension \(n\) (over \(\mathbb{C}\)).
3.4.2 Inner Product
Inner product or scalar product on \(\mathbb{C}^n\) is defined by \[\begin{align*} (\underline{z}, \underline{w}) &= \sum_j \bar{z}_j w_j = \bar{z}_1 w_1 + \dots + \bar{z}_n w_n \end{align*}\]
3.4.2.1 Properties
hermitian \[\begin{align*} (\underline{w}, \underline{z}) = \overline{(\underline{z}, \underline{w})} \end{align*}\]
linear/ anti-linear \[\begin{align*} (\underline{z}, \lambda \underline{w} + \lambda' \underline{w}') &= \lambda (\underline{z}, \underline{w}) + \lambda' (\underline{z}, \underline{w}') \\ (\mu \underline{z} + \mu' \underline{z}', \underline{w}) &= \bar{\mu} (\underline{z}, \underline{w}) + \overline{\mu}' (\underline{z}', \underline{w}) \end{align*}\]
positive definite \[\begin{align*} (\underline{z}, \underline{z}) &= \sum_i |z_i|^2 \in \mathbb{R}_{\geq 0} \\ &= 0 \iff \underline{z} = \underline{0} \end{align*}\] Define length or norm of \(\underline{z}\) to be \(|\underline{z}| \geq 0\) with \(|\underline{z}|^2 = (\underline{z}, \underline{z})\).
Define \(\underline{z}, \underline{w} \in \mathbb{C}^n\) to be orthogonal if \((\underline{z}, \underline{w}) = 0\).
Note, the standard basis \(\{ \underline{e}_j \}\) for \(\mathbb{C}^n\) (see definitions) is orthonormal
\[\begin{align*}
(\underline{e}_i, \underline{e}_j) = \delta_{ij}.
\end{align*}\]
Also if \(\underline{z}_1, \underline{z}_2, \dots, \underline{z}_k\) are non-zero and orthogonal in sense above, then they are linearly independent over \(\mathbb{C}\) (same argument as in real case).
Example 3.8 Complex inner product on \(\mathbb{C}\) (\(n = 1\)) is \[\begin{align*} (z, w) &= \bar{z} w \\ \text{Let } z &= a_1 + i a_2,\ w = b_1 + i b_2 \\ \text{Then } \underline{a} &= (a_1, a_2) \in \mathbb{R}^2,\ \underline{b} = (b_1, b_2) \in \mathbb{R}^2 \text{ the corresponding vectors} \\ \bar{z} w &= (a_1 b_1 + a_2 b_2) + i (a_1 b_2 - a_2 b_1) \\ &= \underline{a} \cdot \underline{b} + i [\underline{a}, \underline{b}] \end{align*}\] recover scalar dot and scalar cross product in \(\mathbb{R}^2\).
3.1.3 Comments
Inner product on \(\mathbb{R}^n\) \[\begin{align*} \underline{a} \cdot \underline{b} = \delta_{ij} a_i b_j \hspace{0.5cm} \left(\sum \text{ convention and } i, j = 1, \dots, n \right) \end{align*}\] Component definition matches geometrical definition for n = 3 Scalar or Dot Product.
In \(\mathbb{R}^3\) we also have a cross product with component definition \((\underline{a} \wedge \underline{b})_i = \epsilon_{ijk} a_j b_k\) (geometric definition given in Vector or Cross Product)
In \(\mathbb{R}^n\) we have \(\epsilon_{\underbrace{ij...l}_\text{$n$ indices}}\) (totally antisymmetric). Cannot use this to define vector-valued product except in \(n = 3\). But in \(\mathbb{R}^2\) we have \(\epsilon_{ij}\) with \(\epsilon_{12} = -\epsilon_{21} = 1\) and we can use this to define an additional scalar cross product in 2d.
\[\begin{align*} [\underline{a}, \underline{b}] &= \epsilon_{ij} a_i b_j \\ &= a_1 b_2 - a_2 b_1 \text{ for } \underline{a}, \underline{b} \in \mathbb{R}^2 \end{align*}\] Geometrically, this gives (signed) area of parallelogram \([\underline{a}, \underline{b}] = |\underline{a}| |\underline{b}| \sin \theta\).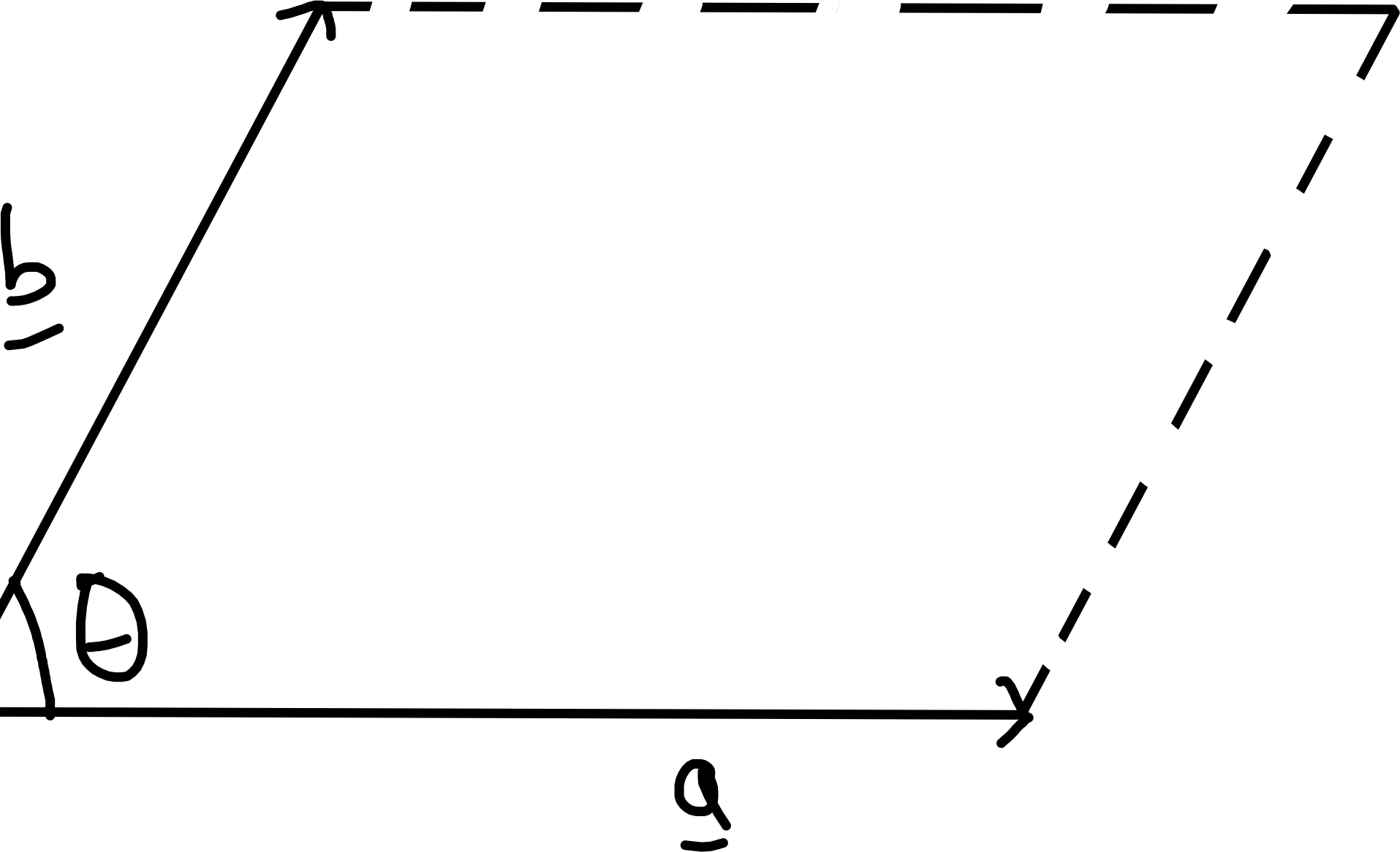 Compare with \([\underline{a}, \underline{b}, \underline{c}] = \underline{a} \cdot \underline{b} \wedge \underline{c} = \epsilon_{ijk} a_i b_j c_k\) which is the (signed) volume of a parallelepiped.
Compare with \([\underline{a}, \underline{b}, \underline{c}] = \underline{a} \cdot \underline{b} \wedge \underline{c} = \epsilon_{ijk} a_i b_j c_k\) which is the (signed) volume of a parallelepiped.