2 Vectors in 3 Dimensions

A vector is a quantity with magnitude and direction (e.g. force, electric and magnetic fields) - all examples modelled on position. We take a geometrical approach to position vectors in 3d space based on standard (Euclidean) notions of points, lines, planes, length, angle etc. Chose point \(O\) as origin, the points \(A\), \(B\) have position vectors \[\begin{align*} \underline{a} = \overrightarrow{OA},\ \underline{b} = \overrightarrow{OB} \end{align*}\] lengths denoted by \(|\underline{a}| = | \overrightarrow{OA}|\), \(\underline{O}\) is the position vector for \(O\).

2.1 Vector Addition and Scalar Multiplication

1. Scalar Multiplication Given \(\underline{a}\), position vector for \(A\) and a scalar \(\lambda \in \mathbb{R}\), \(\lambda \underline{a}\) is position vector of point \(A'\) on \(OA\) with \[\begin{align*} |\lambda \underline{a}| = |\overrightarrow{OA'}| = |\lambda| |\underline{a}| \end{align*}\] as shown Say \(\underline{a}\) and \(\underline{b}\) are parallel, \(\underline{a} \parallel \underline{b} \iff \underline{a} = \lambda \underline{b}\) or \(\underline{b} = \lambda \underline{a}\). Definition allows \(\lambda \leq 0\) so \(\underline{a} \parallel \underline{0}\) for any \(\underline{a}\).

2. Addition Given \(\underline{a}, \underline{b}\) position vectors of \(A, B\) construct a parallelogram \(OACB\) and define \(\underline{a} + \underline{b} = \underline{c}\), position vector of point \(C\), provided \(\underline{a} \nparallel \underline{b}\); if \(\underline{a} \parallel \underline{b}\) then we can write \(\underline{a} = \alpha \underline{u}\), \(\underline{b} = \beta \underline{u}\) for some \(\underline{u}\) and then \(\underline{a} + \underline{b} = (\alpha + \beta) \underline{u}\).

3. Properties For any vectors \(\underline{a}, \underline{b}, \underline{c}\) \[\begin{align*} \underline{a} + \underline{0} &= \underline{0} + \underline{a} = \underline{a} & &(\underline{0} \text{ is identity for } +) \\ \exists \; a \text{ such that } \\ \underline{a} + (- \underline{a}) &= (- \underline{a}) + \underline{a} = \underline{0} & &(-\underline{a} \text{ is the inverse for } \underline{a}) \\ \underline{a} + \underline{b} &= \underline{b} + \underline{a} & &(+ \text{ is commutative}) \\ \underline{a} + (\underline{b} + \underline{c} ) &= ( \underline{a} + \underline{b} ) + \underline{c} & &(+ \text{ is associative}) \\ \lambda ( \underline{a} + \underline{b}) &= \lambda \underline{a} + \lambda \underline{b} &&\\ (\lambda + \mu) \underline{a} &= \lambda \underline{a} + \mu \underline{a} &&\\ \lambda (\mu \underline{a}) &= (\lambda \mu) \underline{a}, & &\lambda, \mu \in \mathbb{R} \end{align*}\] All of these can be checked geometrically, e.g. associativity of vector addition using a parallelepiped

4. Linear Combinations and Span A linear combination of vectors \(\underline{a}, \underline{b}, \dots, \underline{c}\) is an expression \[\begin{align*} \alpha \underline{a} + \beta \underline{b} + \dots + \gamma \underline{c} \text{ for some } \alpha, \beta, \dots, \gamma \in \mathbb{R}. \end{align*}\] The span of a set of vectors is \(\operatorname{span} \{ \underline{a}, \underline{b}, \dots, \underline{c} \} = \{\alpha \underline{a} + \beta \underline{b} + \dots + \gamma \underline{c} : \alpha, \beta, \dots, \gamma \in \mathbb{R} \}\).

If \(a \neq 0\) then \(\operatorname{span} \{ \underline{a} \} = \{ \lambda \underline{a} \}\), which is a line through \(O\) and \(A\).

If \(\underline{a} \nparallel \underline{b}\) (this also means \(\underline{a}, \underline{b} \neq \underline{0}\)) then \(\operatorname{span} \{ \underline{a}, \underline{b}\} = \{ \alpha \underline{a} + \beta \underline{b} : \alpha, \beta \in \mathbb{R}\}\), which is a plane through \(O, A, B\).

2.2 Scalar or Dot Product

1. Definition 2.1 Given \(\underline{a}\) and \(\underline{b}\) let \(\theta\) be the angle between them; then \[\begin{align*} \underline{a} \cdot \underline{b} = | \underline{a} | | \underline{b} | \cos \theta \end{align*}\] scalar or dot product or inner product

   

   Figure 2.1: \(\theta\) defined unless \(|\underline{a}|\) or \(| \underline{b}| = 0\) and then \(\underline{a} \cdot \underline{b} = 0\)

2. Properties \[\begin{align*} \underline{a} \cdot \underline{b} &= \underline{b} \cdot \underline{a} \\ \underline{a} \cdot \underline{a} = |\underline{a}|^2 &\geq 0 \text{ and } = 0 \iff \underline{a} = \underline{0} \\ (\lambda \underline{a}) \cdot \underline{b} &= \lambda (\underline{a} \cdot \underline{b}) = \underline{a} \cdot (\lambda \underline{b}) \\ \underline{a} \cdot ( \underline{b} + \underline{c}) &= \underline{a} \cdot \underline{b} + \underline{a} \cdot \underline{c} \end{align*}\]

3. Interpretation For \(\underline{a} \neq \underline{0}\), consider \(\underline{u} = \frac{\underline{a}}{|\underline{a}|}\) \[\begin{align*} \underline{u} \cdot \underline{b} = \frac{1}{|\underline{a}|} \underline{a} \cdot \underline{b} \end{align*}\] is the component of \(\underline{b}\) along \(\underline{a}\) We can resolve \(\underline{b} = \underline{b}_\parallel + \underline{b}_\perp\). \(\underline{b}_\parallel = (\underline{b} \cdot \underline{u}),\ \underline{b}_\perp = b - (\underline{b} \cdot \underline{u})\) where \(\underline{u} = \frac{\underline{a}}{|\underline{a}|}\). Note \(\underline{a} \cdot \underline{b} = \underline{a} \cdot \underline{b}_\parallel\).   In general, vectors \(\underline{a}\) and \(\underline{b}\) are orthogonal or perpendicular, written \(\underline{a} \perp \underline{b} \iff \underline{a} \cdot \underline{b} = 0\).

2.3 Orthonormal Bases and Components

Choose vectors \(\underline{e}_1, \underline{e}_2, \underline{e}_3\) that are orthonormal i.e. each of unit length and mutually perpendicular. \[\begin{align*} \underline{e}_i \cdot \underline{e}_j = \begin{cases} 1 & \text{if } i = j \\ 0 & \text{if } i \neq j \end{cases} \end{align*}\] This is equivalent to choosing Cartesian axes along these directions, \(\{ \underline{e}_i \}\) is a basis: any vector can be expressed \[\begin{align*} \underline{a} = \sum_{i} a_i \underline{e}_i = a_1 \underline{e}_1 + a_2 \underline{e}_2 + a_3 \underline{e}_3 \end{align*}\] and each component is uniquely determined \[\begin{align*} a_i = \underline{e}_i \cdot \underline{a}. \end{align*}\]

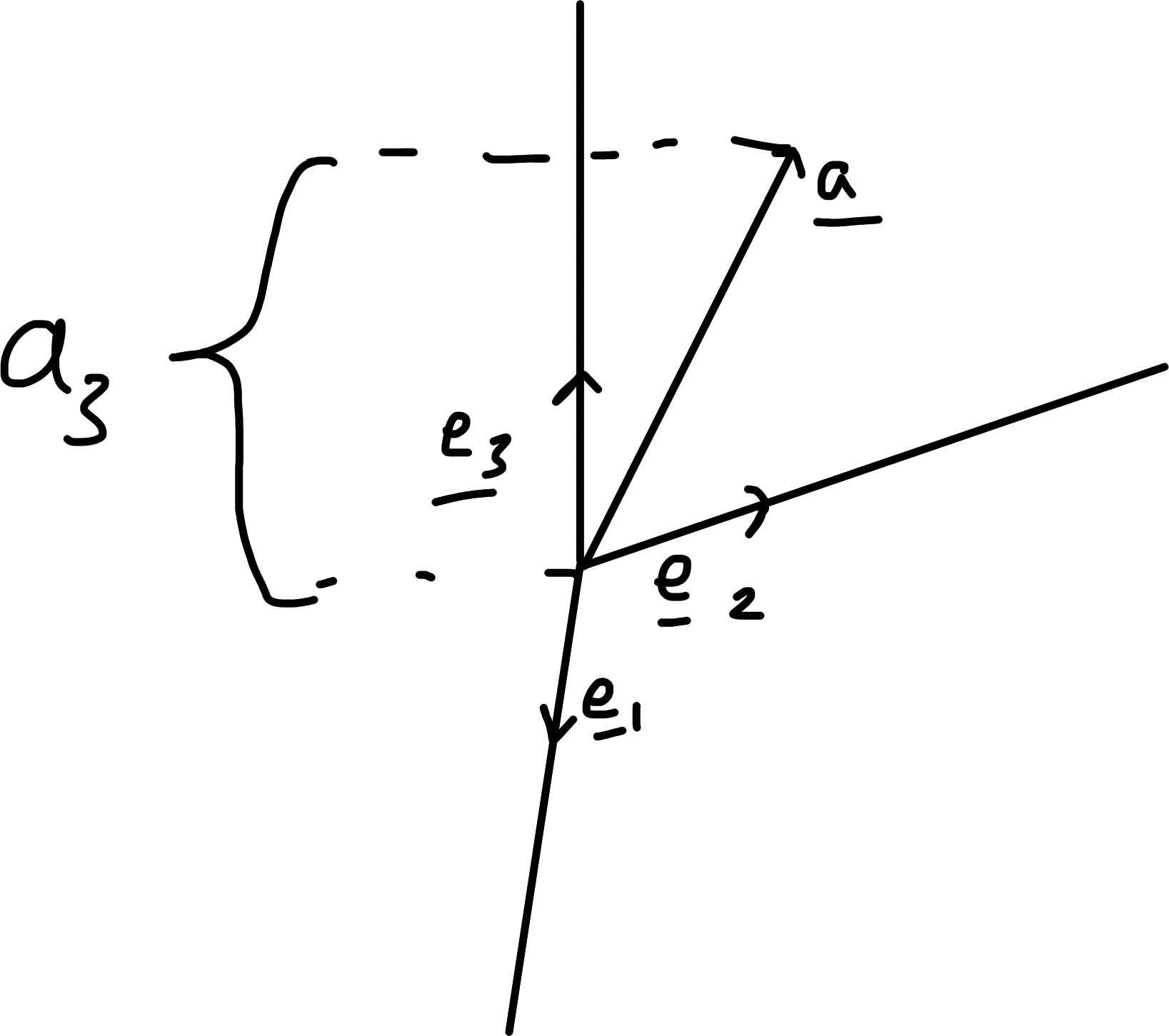
Each \(\underline{a}\) can now be identified with a set of components in \[\begin{align*} \begin{pmatrix} a_1 & a_2 & a_3 \end{pmatrix} \text{ or } \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \end{align*}\]

Note \[\begin{align*} \underline{a} \cdot \underline{b} &= \left( \sum_i a_i \underline{e}_i \right) \cdot \left( \sum_j b_j \underline{e}_j \right) \\ &= a_1 b_1 + a_2 b_2 + a_3 b_3 \\ |\underline{a}|^2 &= a_1^2 + a_2^2 + a_3^2 \quad \text{(Pythagoras)} \end{align*}\] \(\underline{e}_1, \underline{e}_2, \underline{e}_3\) are also often written \(\underline{i}, \underline{j}, \underline{k}\).

2.4 Vector or Cross Product

1. Definition 2.2 Given \(\underline{a}\) and \(\underline{b}\), let \(\theta\) be the angle between them measured in the sense shown relative to a unit normal \(\underline{n}\) to the plane they span; then \[\begin{align*} \underline{a} \wedge \underline{b} = \underline{a} \times \underline{b} = |\underline{a}| | \underline{b}| \sin \theta \, \underline{n} \end{align*}\] is vector or cross product.¹

2. Properties

\[\begin{align*} \underline{a} \wedge \underline{b} &= - \underline{b} \wedge \underline{a} \\ (\lambda \underline{a}) \wedge \underline{b} &= \lambda (\underline{a} \wedge \underline{b}) = \underline{a} \wedge (\lambda \underline{b}) \\ \underline{a} \wedge (\underline{b} + \underline{c}) &= \underline{a} \wedge \underline{b} + \underline{a} \wedge \underline{c} \\ \underline{a} \wedge \underline{b} &= \underline{0} \iff \underline{a} \parallel \underline{b} \\ \underline{a} \wedge \underline{b} &\perp \underline{a} \text{ and } \underline{b} \\ \underline{a} \cdot (\underline{a} \wedge \underline{b}) &= \underline{b} \cdot (\underline{a} \wedge \underline{b}) = 0 \end{align*}\]

3. Interpretations

• \(\underline{a} \wedge \underline{b}\) is the vector area shown: \(|\underline{a} \wedge \underline{b}|\) is the scalar area. The direction of the normal \(\underline{n}\) gives orientation of the parallelogram in space.

• Fix \(\underline{a}\) and consider \(\underline{x} \perp \underline{a}\); then \(\underline{x} \mapsto \underline{a} \wedge \underline{x}\) scales \(| \underline{x} |\) by a factor \(|\underline{a}|\) and rotates \(\underline{x}\) by \(\pi / 2\) in the plane \(\perp \underline{a}\) as shown:

4. Component expressions Consider \(\underline{e}_1, \underline{e}_2, \underline{e}_3\) orthonormal basis as in Orthonormal Bases and Components but assume in addition \[\begin{align*} \underline{e}_1 \wedge \underline{e}_2 = \underline{e}_3 = -\underline{e}_2 \wedge \underline{e}_1 \\ \underline{e}_2 \wedge \underline{e}_3 = \underline{e}_1 = -\underline{e}_3 \wedge \underline{e}_2 \\ \underline{e}_3 \wedge \underline{e}_1 = \underline{e}_2 = -\underline{e}_1 \wedge \underline{e}_3 \end{align*}\] (all equalities follow from any one). This is called a right-handed orthonormal basis.

Now for \[\begin{align*} \underline{a} &= \sum_{i} a_i \underline{e}_i = a_1 \underline{e}_1 + a_2 \underline{e}_2 + a_3 \underline{e}_3 \\ \underline{b} &= \sum_j b_j \underline{e}_j = b_1 \underline{e}_1 + b_2 \underline{e}_2 + b_3 \underline{e}_3 \\ \underline{a} \wedge \underline{b} &= (a_2 b_3 - a_3 b_2)\underline{e}_1 + (a_3 b_1 - a_1 b_3) \underline{e}_2 + (a_1 b_2 - a_2 b_1) \underline{e}_3 \end{align*}\]

2.5 Triple products

1. Scalar Triple Product

Definition 2.3 \[\begin{align*} \underline{a} \cdot (\underline{b} \wedge \underline{c}) &= \underline{b} \cdot (\underline{c} \wedge \underline{a}) = \underline{c} \cdot ( \underline{a} \wedge \underline{b}) \\ &= - \underline{a} \cdot (\underline{c} \wedge \underline{b}) = - \underline{b} \cdot (\underline{a} \wedge \underline{c}) = - \underline{c} \cdot (\underline{b} \wedge \underline{a}) \\ &= \left[ \underline{a}, \underline{b}, \underline{c} \right] \end{align*}\]

Interpretation: \(|\underline{c} \cdot \underline{a} \wedge \underline{b}|\) is the volume of a parallelepiped shown The “signed volume” is \(\underline{c} \cdot \underline{a} \wedge \underline{b}\); if \(\underline{c} \cdot \underline{a} \wedge \underline{b} > 0\) then we say \(\underline{a}, \underline{b}, \underline{c}\) is a right-handed set

Note: \(\underline{a} \cdot \underline{b} \wedge \underline{c} = 0\) iff \(\underline{a}, \underline{b}, \underline{c}\) are co-planar meaning one of them lies in the plane spanned by the other two. e.g. \(\underline{c} = \alpha \underline{a} + \beta \underline{b}\) belonging to \(\operatorname{span} \{ a, b \}\)

Example 2.1 \[\begin{align*} \underline{a} &= \begin{pmatrix}2 & 0 & -1\end{pmatrix} \\ \underline{b} &= \begin{pmatrix}7 & -3 & 5 \end{pmatrix} \\ \implies \underline{a} \wedge \underline{b} &= (0.5 - (-1)(-3)) \underline{e}_1 + ((-1)7 - 2.5) \underline{e}_2 + (2(-3) - 0.7) \underline{e}_3 \\ &= \begin{pmatrix}-3 & -17 & -6 \end{pmatrix} \end{align*}\] To test whether \(\underline{a}, \underline{b}, \underline{c}\) are co-planar with \(\underline{c} = \begin{pmatrix}3 & -3 & 7 \end{pmatrix}\). \[\begin{align*} \underline{c} \cdot \underline{a} \wedge \underline{b} &= 3(-3) + (-3)(-17) + 7(-6) \\ &= 0; \end{align*}\] consistent with \(\underline{c} = \underline{b} - 2 \underline{a}\).

2. Vector Triple Product \[\begin{align*} \underline{a} \wedge (\underline{b} \wedge \underline{c}) &= (\underline{a} \cdot \underline{c}) \underline{b} - (\underline{a} \cdot \underline{b}) \underline{c} \\ (\underline{a} \wedge \underline{b}) \wedge \underline{c} &= (\underline{a} \cdot \underline{c}) \underline{b} - (\underline{b} \cdot \underline{c}) \underline{a} \end{align*}\]

Forms of RHS is constrained by definitions above, and we could check explicitly. We will return to these formulae using index notation and summation convention.

2.6 Lines, Planes and Other Vector Equations

2.6.1 Lines

General point on a line through \(\underline{a}\) with direction \(\underline{u} \neq \underline{0}\) has position vector \[\begin{align*} \underline{r} = \underline{a} + \lambda \underline{u},\ \lambda \in \mathbb{R} \end{align*}\] in parametric form.

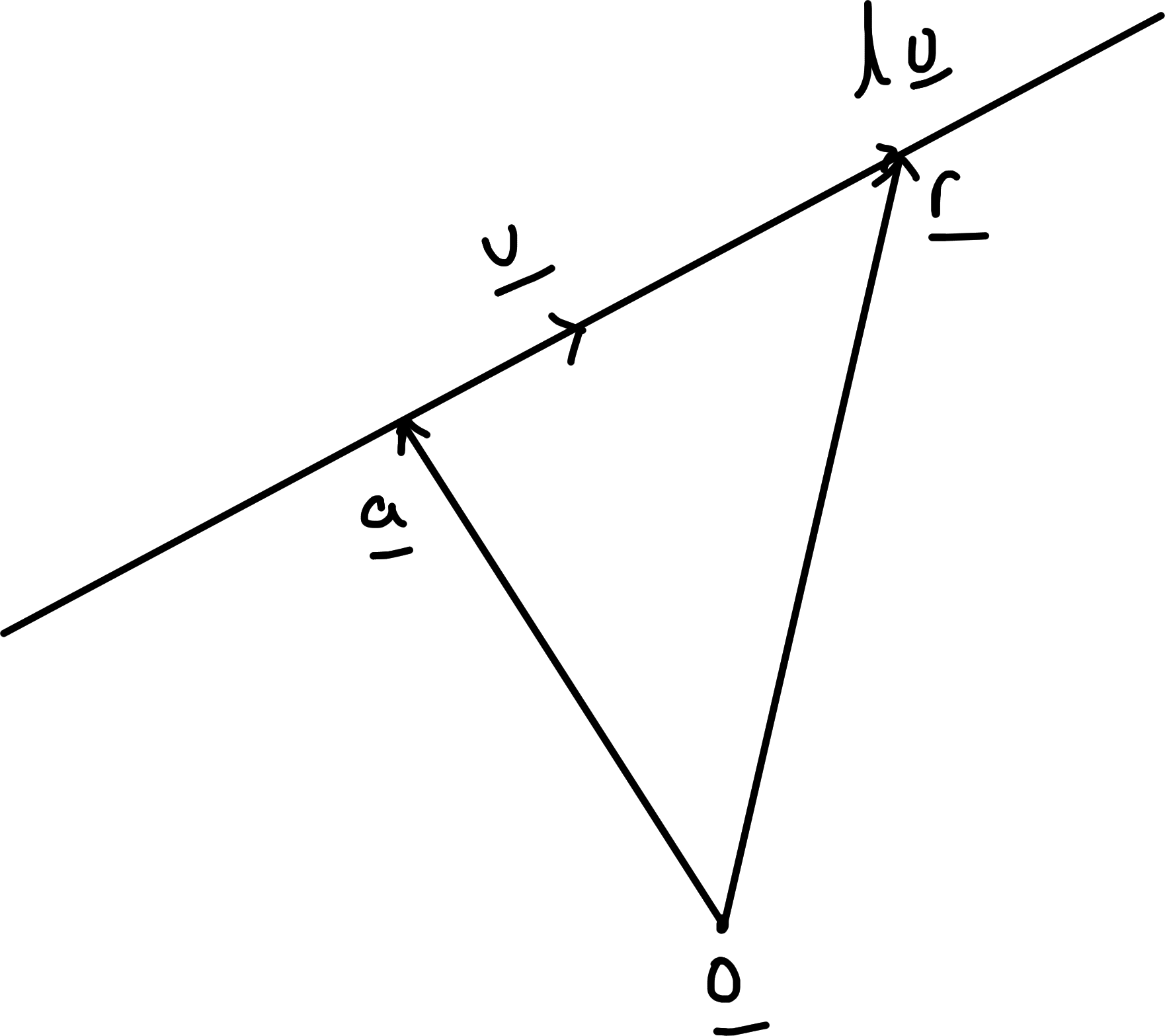
Alternative form without parameter \(\lambda\) obtained by crossing with \(\underline{u}\): \[\begin{align*} \underline{u} \wedge \underline{r} = \underline{u} \wedge \underline{a} \end{align*}\] Conversely \(\underline{u} \wedge (\underline{r} - \underline{a}) = \underline{0}\) and this holds \(\iff \underline{r} - \underline{a} = \lambda \underline{u}\) for some \(\lambda\).

Now consider \[\begin{align*} \underline{u} \wedge \underline{r} &= \underline{c} \text{ where } \underline{u}, \underline{c} \text{ are given vectors and } \underline{u} \neq \underline{0} \\ \text{Note } \underline{u} \cdot (\underline{u} \wedge \underline{r}) &= \underline{u} \cdot \underline{c} \\ &= 0 \end{align*}\] If \(\underline{u} \cdot \underline{c} \neq 0\) then we have a contradiction i.e. no solutions. If \(\underline{u} \cdot \underline{c} = 0\), try a particular solution by considering \[\begin{align*} \underline{u} \wedge (\underline{u} \wedge \underline{c}) &= \overbrace{(\underline{u} \cdot \underline{c})}^0 \underline{u} - (\underline{u} \cdot \underline{u}) \underline{c} \\ &= - |\underline{u}|^2 \underline{c} \end{align*}\]

Hence \(\underline{a} = - \frac{1}{|\underline{u}|^2} (\underline{u} \wedge \underline{c})\) is a solutions. The general solution is \[\begin{align*} \underline{r} = \underline{a} + \lambda \underline{u} \end{align*}\] as \(\underline{u} \wedge (\underline{a} + \lambda \underline{u}) = \underline{u} \wedge \underline{a}\)

2.6.2 Planes

The general point on a plane through \(\underline{a}\) with directions \(\underline{u}, \underline{v}\) in plane (\(\underline{u} \nparallel \underline{v}\)) has position vector \[\begin{align*} \underline{r} = \underline{a} + \lambda \underline{u} + \mu \underline{v}, \text{ where } \lambda, \mu \in \mathbb{R} \end{align*}\] in parametric form.

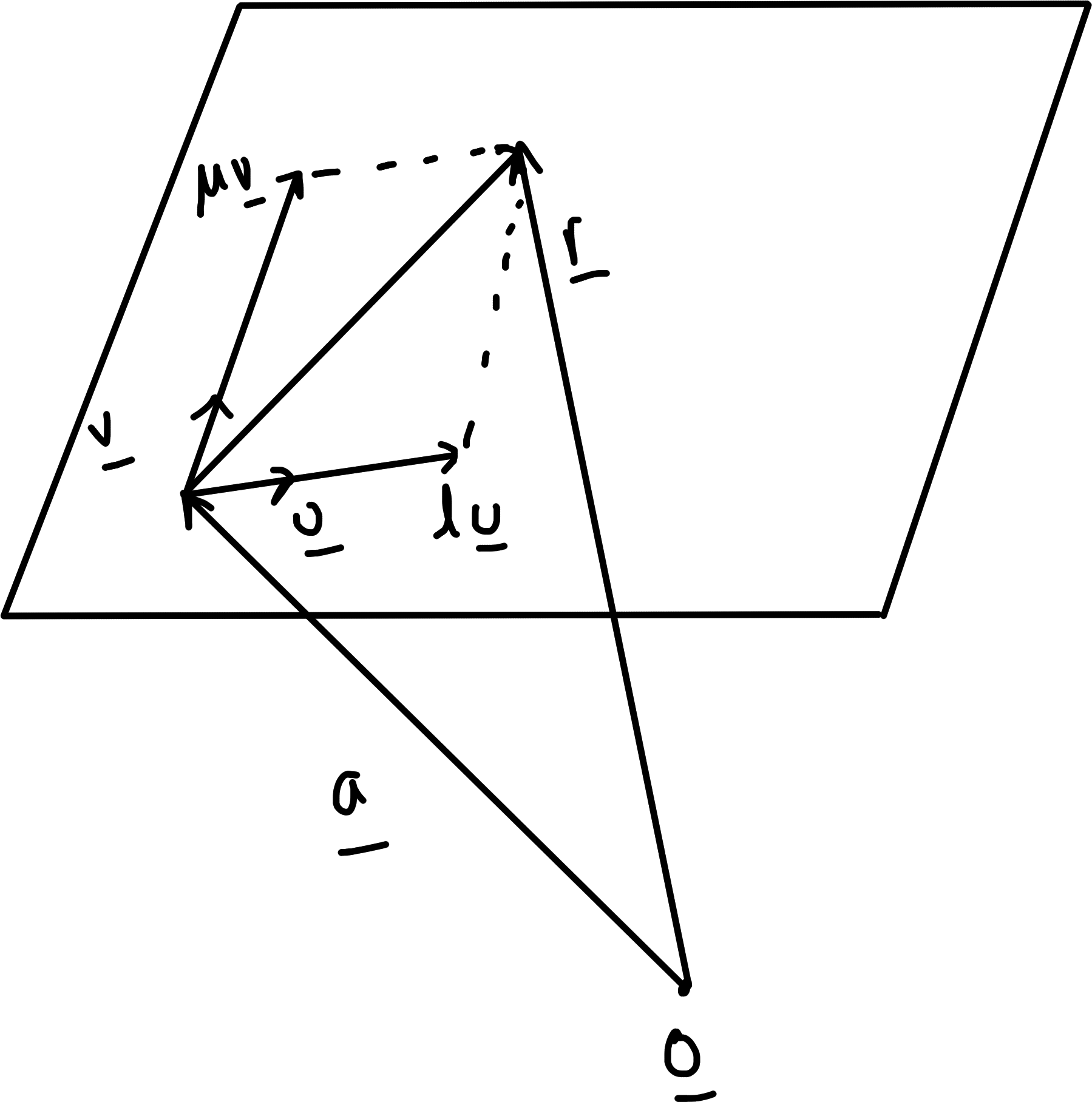
An alternative form without parameters is obtained by by dotting with a normal vector \(\underline{n} = \underline{u} \wedge \underline{v} \neq 0\) (since \(\underline{u} \nparallel \underline{v}\) but is not necessarily a unit vector).

This gives \[\begin{align*} \underline{n} \cdot \underline{r} &= \underline{n} \cdot \underline{a} \\ &= \kappa \text{ (a constant)} \end{align*}\] Note component of \(\underline{r}\) along \(\underline{n}\) is \[\begin{align*} \frac{\underline{n} \cdot \underline{r}}{|\underline{n}|} = \frac{\kappa}{|\underline{n}|} \end{align*}\]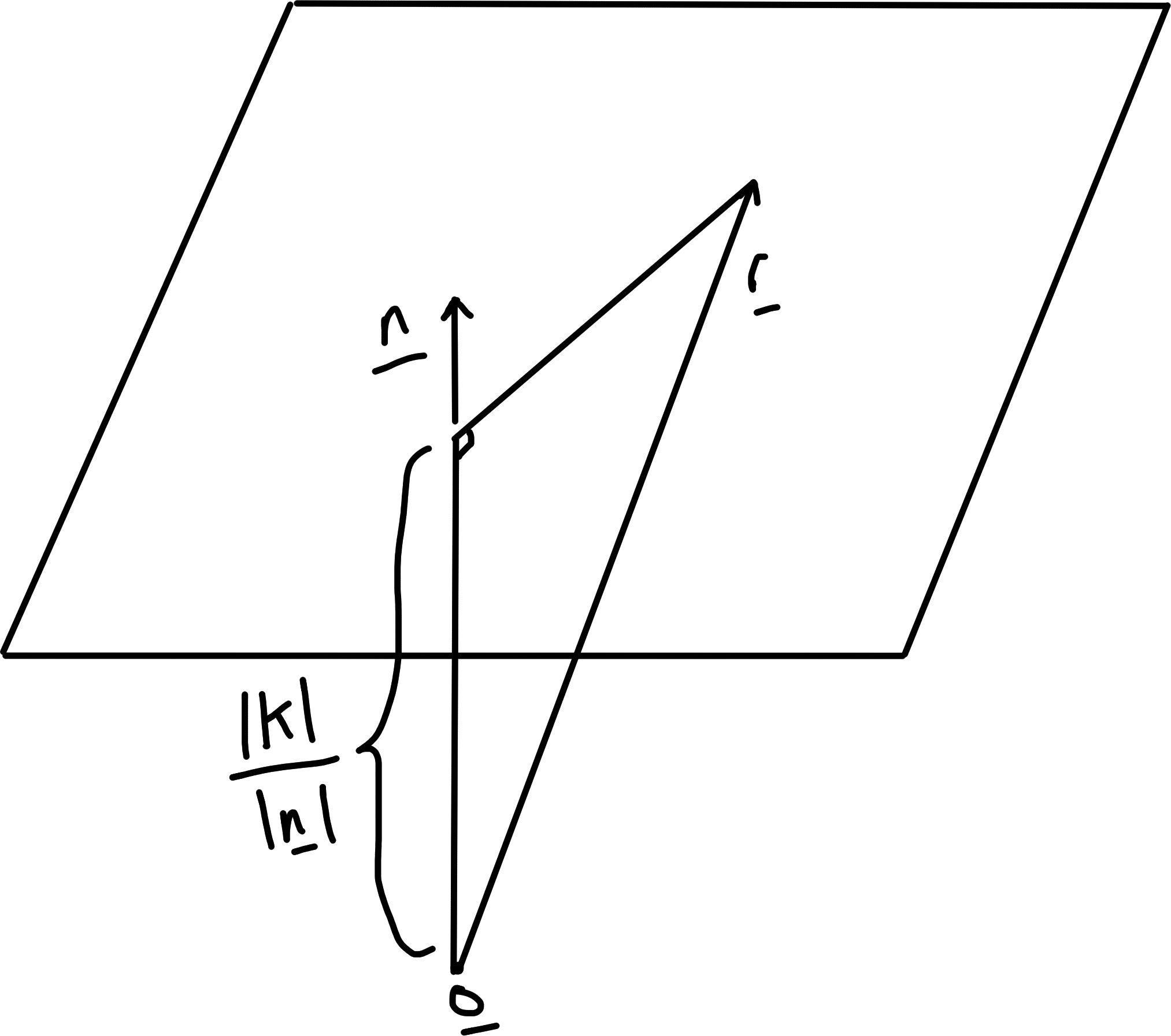

Figure 2.2: Clearly a plane

Moreover \(|\kappa| / |\underline{n}|\) is perpendicular distance of plane from \(\underline{0}\).

2.6.3 Other Vector Equations

Consider equations for \(\underline{r}\) (unknown) written in vector notation with given constant vectors.

Possible approaches:

• We can re-write and convert to some standard form

Example 2.2 \[\begin{align*} |\underline{r}|^2 + \underline{r} \cdot \underline{a} &= k \\ \text{Complete the square:} \\ \left| \underline{r} + \frac{1}{2} \underline{a} \right|^2 &= \left( \underline{r} + \frac{1}{2} \underline{a} \right) \cdot \left( \underline{r} + \frac{1}{2} \underline{a} \right) \\ &= k + \frac{1}{4} |\underline{a}|^2. \end{align*}\] This is the equation of a sphere, centre \(-\frac{1}{2} \underline{a}\) and radius \((k + \frac{1}{4} |\underline{a}|^2)^{1 / 2}\) provided \(k + \frac{1}{4} |\underline{a}|^2 > 0\)

For equations linear in \(\underline{r}\)

• Try dotting and crossing with constant vectors to learn more.

Example 2.3 Another example of a vector equation is \[\begin{align} \underline r + \underline a \times (\underline b \times \underline r) = \underline c \tag{2.1} \end{align}\] where \(\underline a, \underline b, \underline c\) are fixed. We can dot with \(\underline a\) to eliminate the second term: \[\begin{align} \underline a \cdot \underline r = \underline a \cdot \underline c \tag{2.2} \end{align}\] Note that using the dot product loses information — this is simply a tool to make deductions; (2.2) does not contain the full information of (2.1), i.e. (2.2) \(\ \not\!\!\!\!\implies\) (2.1). Combining (2.1) and (2.2), and using the formula for the vector triple product, we get \[\begin{align} \underline r + (\underline a \cdot \underline r) \underline b - (\underline a \cdot \underline b) \underline r & = \underline c \tag{2.3} \\ \implies \underline r + (\underline a \cdot \underline c) \underline b - (\underline a \cdot \underline b) \underline r & = \underline c \notag \end{align}\] This eliminates the dependency on \(\underline r\) inside the dot product. Now, we can factorise, leaving \[\begin{align} (1 - \underline a \cdot \underline b) \underline r = \underline c - (\underline a \cdot \underline c) \underline b \tag{2.4} \end{align}\]

1. If \(1 - \underline a \cdot \underline b \neq 0\) then \(\underline r\) has a single solution, \(\underline{r} = (\underline{c} - (\underline{a} \cdot \underline{c}) \underline{b} ) / (1 - \underline{a} \cdot b)\), a point.

2. If \(1 - \underline{a} \cdot \underline{b} = 0\) and \(\underline c - (\underline a \cdot \underline c) \underline b \neq 0\) implies (2.4) is inconsistent so no solution

3. If \(1 - \underline{a} \cdot \underline{b} = 0\) and \(\underline c - (\underline a \cdot \underline c) \underline b = 0\) We can now combine this expression for \(\underline c\) into (2.3) and eliminate the \((1- \underline a \cdot \underline b)\) term, to get \[\begin{align*} (\underline a \cdot \underline r - \underline a \cdot \underline c) \underline b = \underline 0 \end{align*}\] This shows us that (given that \(\underline b\) is non-zero) the solutions to the equation are given by (2.2), which is the equation of a plane, so (2.2) \(\implies\) (2.1).

• Can try expressing \(\underline{r} = \alpha \underline{a} + \beta \underline{b} + \gamma \underline{c}\) for some non-co-planar \(\underline{a}, \underline{b}, \underline{c}\) and solve for \(\alpha, \beta, \gamma\).

• Can choose basis and use index/ matrix notation.

2.7 Index (suffix) Notation and the Summation convention

2.7.1 Components; \(\delta\) and \(\epsilon\)

Write vectors \(\underline{a}, \underline{b}, \dots\), in terms of components \(a_i, b_i, \dots\), wrt. an orthonormal, right-handed basis \[\begin{align*} \underline{e}_1, \underline{e}_2, \underline{e}_3. \end{align*}\] Indices or suffices \(i, j, k, l, p, q \dots\) take values \(1, 2, 3\).

Then \[\begin{align*} && \underline{c} &= \alpha \underline{a} + \beta \underline{b} \\ &\iff & c_i &= [\alpha \underline{a} + \beta \underline{b}] \\ && &= \alpha a_i + \beta b_i \text{ for } i = 1, 2, 3 \textbf{ free index} \\ && \underline{a} \cdot \underline{b} &= \sum_i a_i b_i = \sum_j a_j b_j \\ && \underline{x} &= \underline{a} + (\underline{b} \cdot \underline{c}) \underline{d} \\ &\iff & x_j &= a_j + \left( \sum_k b_k c_k \right) d_j \text{ for } j = 1, 2, 3 \text{ free index} \end{align*}\]

Definition 2.4 (Kronecker Delta) \[\begin{align*} \delta_{ij} &= \begin{cases} 1 & \text{if } i = j \\ 0 & \text{else}\\ \end{cases} \\ \delta_{ij} &= \delta_{ji} \text{ symmetric} \\ \text{Written out as an array} &\text{ or matrix}\\ \begin{pmatrix} \delta_{11} & \delta_{12} & \delta_{13} \\ \delta_{21} & \delta_{22} & \delta_{23} \\ \delta_{31} & \delta_{32} & \delta_{33} \end{pmatrix} &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ \text{Then } \underline{e}_i \cdot \underline{e}_j &= \delta_{ij} \\ \text{and } \underline{a} \cdot \underline{b} &= \left( \sum_i a_i \underline{e}_i \right) \cdot \left( \sum_j b_j \underline{e}_j \right) \\ &= \sum_{ij} a_i b_j \underline{e}_i \cdot \underline{e}_j \\ &= \sum_{ij} a_i b_j \delta_{ij} \\ &= \sum_i a_i b_i \end{align*}\]

Definition 2.5 (Levi-Civita Epsilon) \[\begin{align*} \epsilon_{ijk} &= \begin{cases} + 1 & \text{if } (i, j, k) \text{ is an even permutation of } (1, 2, 3) \\ - 1 & \text{if } (i, j, k) \text{ is an odd permutation of } (1, 2, 3) \\ 0 & \text{else} \end{cases} \\ \text{i.e. } \epsilon_{123} &= \epsilon_{231} = \epsilon_{312} = + 1 \\ \epsilon_{321} &= \epsilon_{213} = \epsilon_{132} = - 1 \\ \epsilon_{ijk} &= 0 \text{ if any two index values match} \end{align*}\] \(\epsilon_{ijk}\) is totally antisymmetric: exchanging any pairs of indices produces a change in sign. Then \[\begin{align*} \underline{e}_i \wedge \underline{e}_j &= \sum_k \epsilon_{ijk} \ \underline{e}_k \\ \text{e.g. } \underline{e}_2 \wedge \underline{e}_1 &= \sum_k \epsilon_{21k} \ \underline{e}_k \\ &= \epsilon_{213} \ \underline{e}_3 \\ &= - \underline{e}_3 \\ \text{And } \underline{a} \wedge \underline{b} &= \left( \sum_i a_i \underline{e}_i \right) \wedge \left( \sum_j b_j \underline{e}_j \right) \\ &= \sum_{ij} a_i b_j \underline{e}_i \wedge \underline{e}_j \\ &= \sum_{ij} a_i b_j \left( \sum_k \epsilon_{ijk} \ \underline{e}_k \right) \\ &= \sum_k \left( \sum_{ij} \epsilon_{ijk} a_i b_j \right) \underline{e}_k \\ \text{Hence } (\underline{a} \wedge \underline{b})_k &= \sum_{ij} \epsilon_{ijk} a_i b_j \\ \text{e.g. } (\underline{a} \wedge \underline{b})_3 &= \sum_{ij} \epsilon_{ij3} a_i b_j \\ &= \epsilon_{123} a_1 b_2 + \epsilon_{213} a_2 b_1 \\ &= a_1 b_2 - a_2 b_1. \end{align*}\]

2.7.2 Summation Convention

With component/ index notation, we observe that indices that appear twice in a given term are (usually) summed over. In the summation convention we omit \(\sum\) signs for repeated indices: the sum is understood.

Example 2.4 \[\begin{align*} a_i \delta_{ij} &= a_1 \delta_{1j} + a_2 \delta_{2j} + a_3 \delta_{3j} \\ &= \begin{cases} a_1 & \text{if } j = 1 \\ a_2 & \text{if } j = 2 \\ a_3 & \text{if } j = 3 \end{cases} \\ a_i \delta_{ij} &= a_j \end{align*}\]

Example 2.5 \[\begin{align*} \underline{a} \cdot \underline{b} &= \delta_{ij} a_i b_j \\ &= a_i b_i \end{align*}\]

Example 2.6 \[\begin{align*} (\underline{a} \wedge \underline{b})_i = \epsilon_{ijk} a_j b_k \end{align*}\]

Example 2.7 \[\begin{align*} \underline{a} \cdot \underline{b} \wedge c &= \epsilon_{ijk} a_i b_j c_k \end{align*}\]

Example 2.8 \[\begin{align*} \delta_{ii} = \delta_{11} + \delta_{22} + \delta_{33} = 3 \end{align*}\]

Example 2.9 \[\begin{align*} \left[ (\underline{a} \cdot \underline{c}) \underline{b} - (\underline{a} \cdot \underline{b}) \underline{c} \right]_i &= (\underline{a} \cdot \underline{c}) \underline{b}_i - (\underline{a} \cdot \underline{b}) \underline{c}_i \\ &= a_j c_j b_i - a_j b_j c_i \end{align*}\]

2.7.3 Rules

1. An index that occurs exactly once in any term must appear once in every term and it can take any value - a free index.

2. An index occurring exactly twice in a given term is summed over - a repeated/ contracted or dummy index.

3. No index can occur more than twice.

2.7.4 Application

Proof of the vector triple product identity. Consider

Proof. \[\begin{align*} \left[ \underline{a} \wedge (\underline{b} \wedge \underline{c}) \right]_i &= \epsilon_{ijk} a_j (\underline{b} \wedge \underline{c})_k \\ &= \epsilon_{ijk} a_j \epsilon_{kpq} b_p c_q \\ &= \epsilon_{ijk} \epsilon_{pqk} a_j b_p c_q \\ \epsilon_{ijk} \epsilon_{pqk} &= \delta_{ip}\delta_{jq} - \delta_{iq} \delta_{jp} \text{ see below} \\ \left[ \underline{a} \wedge (\underline{b} \wedge \underline{c}) \right]_i &= (\delta_{ip}\delta_{jq} - \delta_{iq}\delta_{jp}) a_j b_p c_q \\ &= a_j \delta_{ip} b_p \delta_{jq} c_q - a_j \delta_{jp} b_p \delta_{iq} c_q \\ &= a_j b_i c_j - a_j b_j c_i,\ \delta_{ij} x_j = x_i = \delta_{ji} x_j \\ &= (a_j c_j) b_i - (a_j b_j) c_i \\ &= (\underline{a} \cdot \underline{c}) b_i - (\underline{a} \cdot \underline{b}) c_i \\ &= \left[ (\underline{a} \cdot \underline{c}) \underline{b} - (\underline{a} \cdot \underline{b}) \underline{c} \right]_i \\ \text{True for } i &= 1, 2, 3 \text{ hence} \\ \underline{a} \wedge (\underline{b} \wedge \underline{c}) &= (\underline{a} \cdot \underline{c}) \underline{b} - (\underline{a} \cdot \underline{b}) \underline{c} \end{align*}\]

2.7.5 \(\epsilon \epsilon\) identities

1. \[\begin{align*} \epsilon_{ijk} \epsilon_{pqk} &= \sum_k \epsilon_{ijk} \epsilon_{pqk} \\ &= \delta_{ip}\delta_{jq} - \delta_{iq} \delta_{jp} \\ &= \epsilon_{kij} \epsilon_{kpq} \end{align*}\]² Check: RHS and LHS are both antisymmetric under \(i \leftrightarrow j\) or \(p \leftrightarrow q\). So both sides vanish if \(i = j\) or \(p = q\). Now suffices to check e.g. \(i = p = 1\) and \(j = q = 2\) \[\begin{align*} LHS &= \epsilon_{123} \epsilon_{123} = 1 \\ RHS &= \delta_{11} \delta_{22} - \delta_{12} \delta_{21} = 1 \end{align*}\] or \(i = q = 1\) and \(j = p = 2\) \[\begin{align*} LHS &= \epsilon_{123} \epsilon_{213} = 1(-1) = -1 \\ RHS &= \delta_{12} \delta_{21} - \delta_{11} \delta_{22} = -1 \end{align*}\] All other index choices work similarly, proof by exhaustion.

2. \(\epsilon_{ijk} \epsilon_{pjk} = 2\delta_{ip}\) contract result above \[\begin{align*} \epsilon_{ijk} \epsilon_{pqk} &= \delta_{ip}\delta_{jj} - \delta_{ij} \delta_{jp} \\ &= 3\delta_{ip} - \delta_{ip} \\ &= 2 \delta_{ip} \end{align*}\]

3. \(\epsilon_{ijk} \epsilon_{ijk} = 6\)

---

1. \(\underline{n}\) is defined up to a choice of sign if \(\underline{a} \nparallel \underline{b}\), but changing the sign of \(\underline{n}\) means changing \(\theta\) to \(2\pi - \theta\) so definition is unchanged; \(\underline{n}\) is not defined if \(\underline{a} \parallel \underline{b}\) and \(\theta\) is not defined if \(\underline{a}\) or \(\underline{b} = 0\), but \(\underline{a} \wedge \underline{b} = \underline{0}\) in these cases.↩︎

2. expected to know this and quote it↩︎