1 Complex Numbers
1.1 Definitions
Construct \(\mathbb{C}\) by adding an element \(i\) to real numbers \(\mathbb{R}\), with \[\begin{align*} i^2 = -1. \end{align*}\] Any complex numbers \(z \in \mathbb{C}\) has the form \(z = x + iy\) with \(x, y \in \mathbb{R}\); \(x = \operatorname{Re}(z)\), real part; \(y = \operatorname{Im}(z)\), imaginary part.
\(\mathbb{R} \subset \mathbb{C}\) consisting of elements \(x + i 0 = x\)
In the following, use the notation above and \(z_1 = x_1 + i y_1\), \(z_2 = x_2 + i y_2\) etc.
Addition ( and subtraction) \[\begin{align*} z_1 \pm z_2 = (x_1 \pm x_2) + i (y_1 \pm y_2) \end{align*}\]
Multiplication \[\begin{align*} z_1 z_2 = (x_1 x_2 - y_1 y_2) + i(x_1 y_2 + x_2 y_1) \end{align*}\]
If \(z \neq 0\), observe from the definition \[\begin{align*} z^{\text{-}1} = \frac{x}{x^2 + y^2} - i \frac{y}{x^2 + y^2} \end{align*}\] satisfies \(z z^{\text{-}1} = 1\)
Complex conjugate \[\begin{align*} \overline{z} &= z^{*} = x - iy \\ \operatorname{Re}(z) &= \frac{1}{2} (z + \overline{z}) \\ \operatorname{Im}(z) &= \frac{1}{2i} (z - \overline{z}) \\ \overline{(\overline{z})} &= z \\ \overline{z_1 + z_2} &= \overline{z_1} + \overline{z_2} \\ \overline{z_1 z_2} &= (\overline{z_1}) (\overline{z_2}) \end{align*}\]
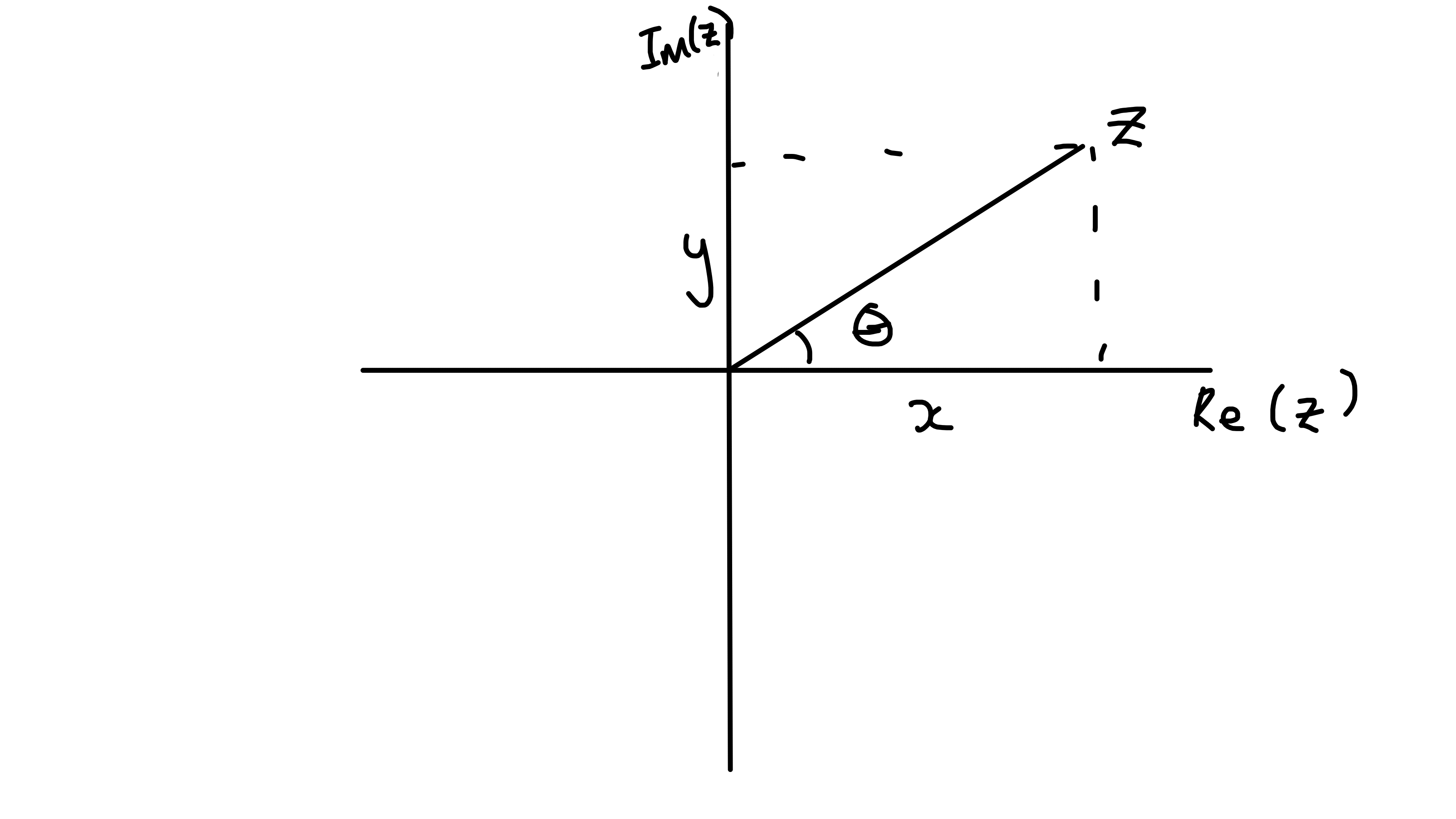
Modulus is defined by \(r = |z|\), real and \(\geq 0\), with \[\begin{align*} r^2 = |z|^2 = z \overline{z} = x^2 + y^2 \end{align*}\]
Argument \(\theta = \arg{z}\), real, defined for \(z \neq 0\) by \[\begin{align*} z = r(\cos \theta + i \sin \theta) \hspace{2cm} \textbf{polar form} \end{align*}\] for some real \(\theta\)
\[\begin{align*} \cos \theta &= \frac{x}{(x^2 + y^2)^{1/2}},\ \sin \theta = \frac{y}{(x^2 + y^2)^{1/2}}, \\ & \implies \tan \theta = \frac{y}{x} \end{align*}\]
\(\arg(z)\) is determined only \(\operatorname{mod} 2 \pi\), i.e. can change \(\theta \to \theta + 2n \pi\) where \(n \in \mathbb{Z}\). To make it unique we can restrict the range, e.g. principal value defined by \(- \pi < \theta \leq \pi\)
- Argand diagram and Complex Plane Plot \(\operatorname{Re}(z)\) and \(\operatorname{Im}(z)\) on orthogonal axes, then \(r = |z|\) and \(\theta = \arg(z)\) are the length and angle shown.
Example 1.1 For \(z = -1 + i \sqrt{3} = 2 (- \frac{1}{2} + i \frac{\sqrt{3}}{2})\), we have \(|z| = 2\) and \(\arg(z) = \frac{2 \pi}{3} + 2 n \pi\) where \(n \in \mathbb{Z}\).
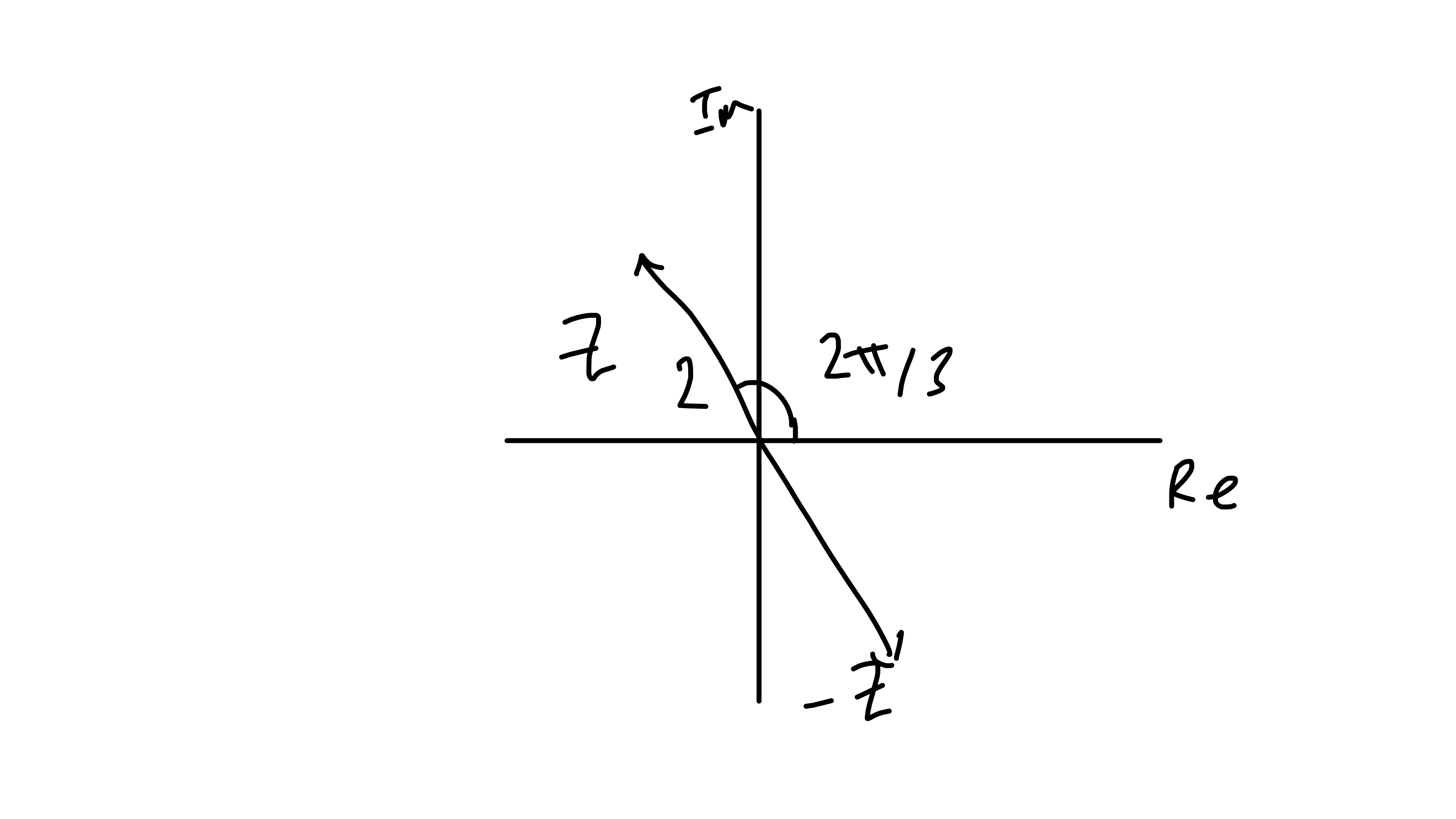
Note \[\begin{align*} \tan \theta = - \sqrt{3} \\ \implies \theta = \frac{2 \pi}{3} + 2 n \pi \\ = \arg(z) \\ \textbf{or } \theta = - \frac{\pi}{3} + 2 n \pi \\ = \arg(-z) \end{align*}\]
1.2 Basic properties and Consequences
- \(\mathbb{C}\) with operations \(+, \times\) is a field, i.e.
- \(\mathbb{C}\) with \(+\) is an abelian group.
- \(\mathbb{C} \setminus \{0\}\) with \(\times\) is an abelian group.
- distributive laws hold, e.g. \(z_1(z_2 + z_3) = z_1 z_2 + z_1 z_3\).
- Fundamental Theorem of Algebra
A polynomial of degree \(n\) with coefficients in \(\mathbb{C}\) can be written as a product of \(n\) linear factors. \[\begin{align*} p(z) &= c_n z^n + \ldots + c_1 z + c_0 \ \ \text{ where } c_i \in \mathbb{C}, c_n \neq 0 \\ &= c_n ( z - \alpha_1) \ldots (z - \alpha_n) \text{ where } \alpha_i \in \mathbb{C}. \end{align*}\]
Hence \(p(z) = 0\) has at least one root and \(n\) roots connected with multiplicity (if we count duplicates as separate).
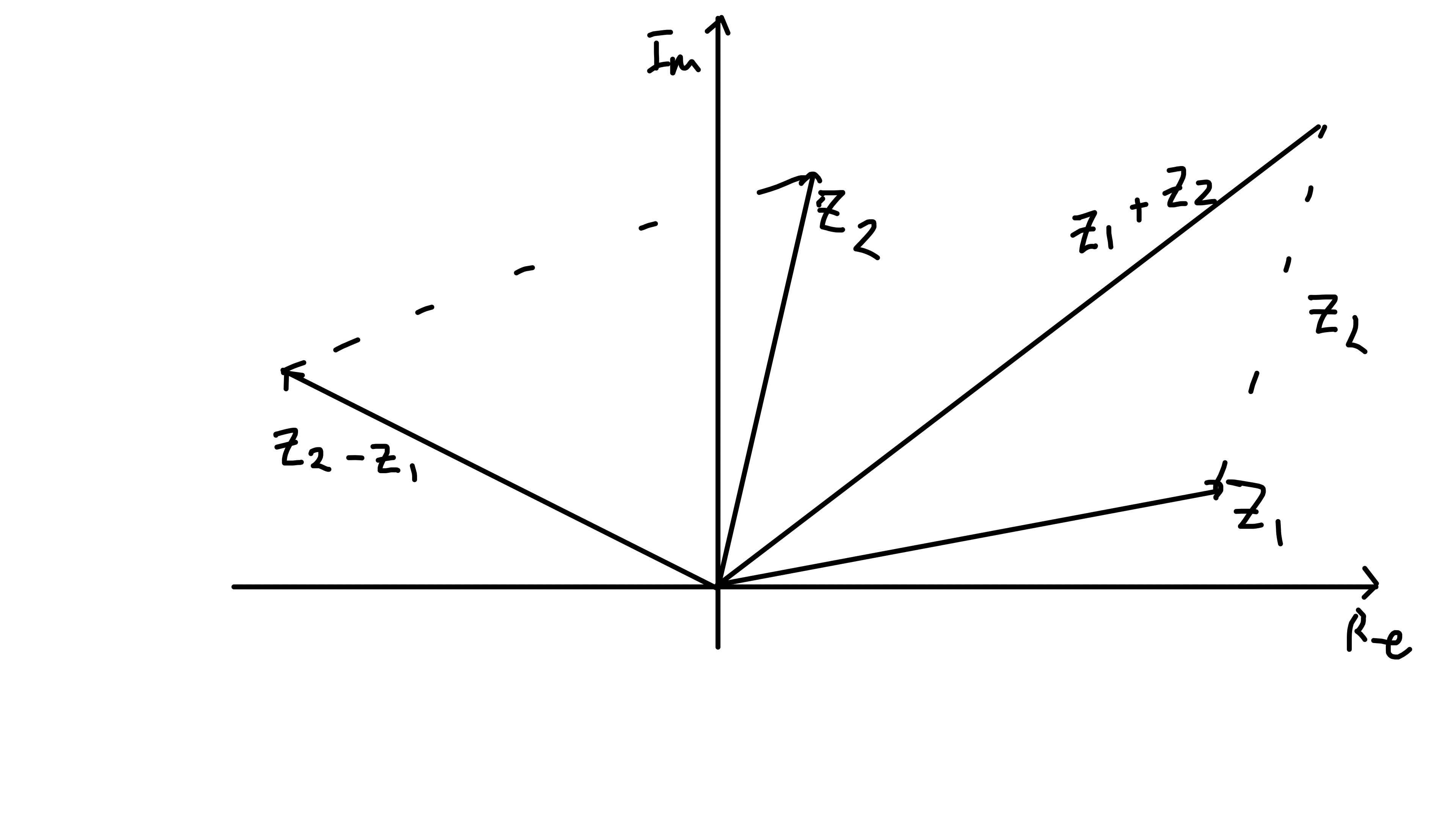
- Addition and subtraction can be viewed as parallelogram constructions
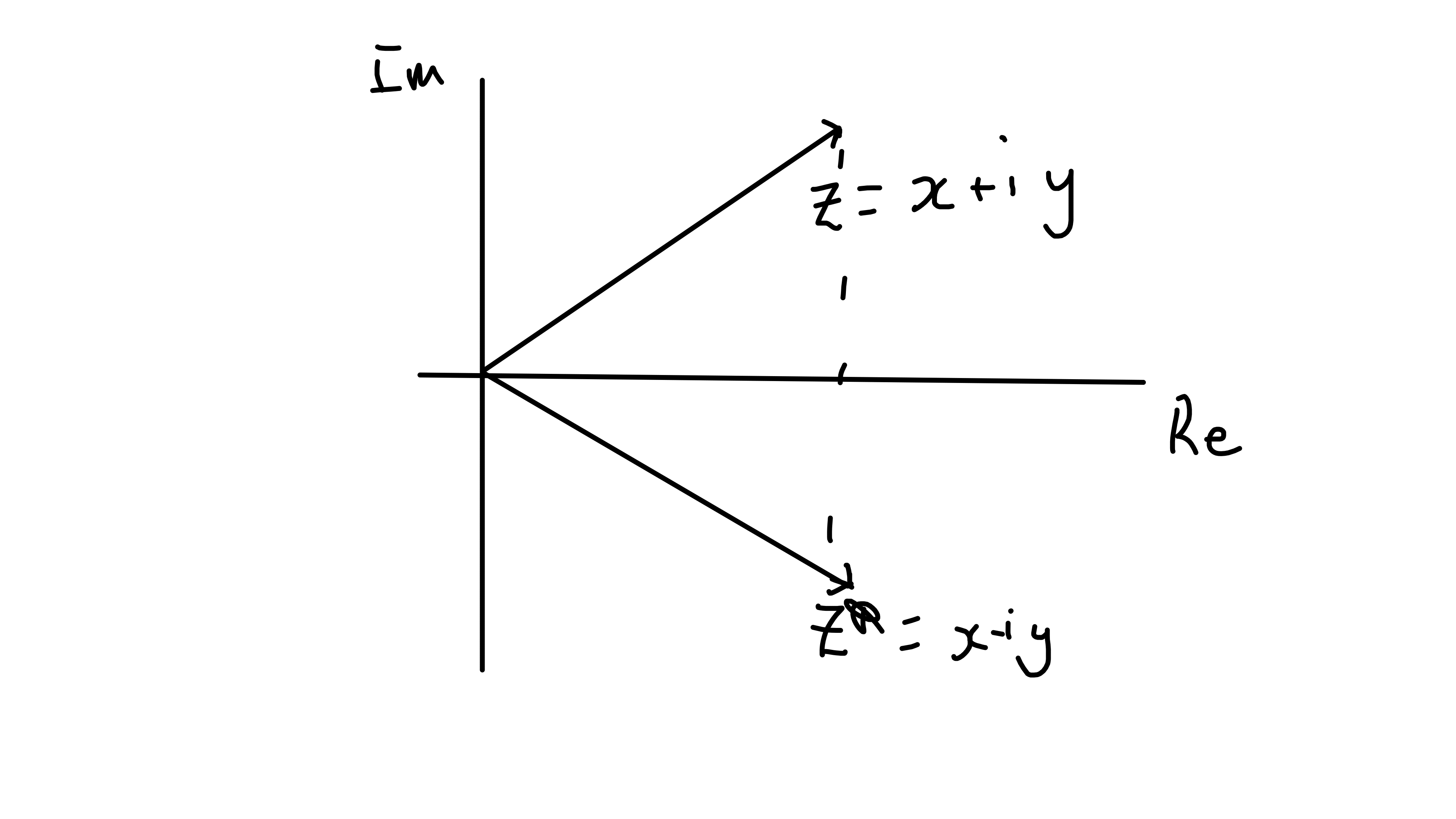
Complex conjugation is reflection in real axis
Proposition 1.1 Modulus/ length obeys composition property \(|z_1 z_2| = |z_1| |z_2|\). Triangle inequality \(|z_1 + z_2| \leq |z_1| + |z_2|\)
Proof (Triangle inequality). Compare \[\begin{align*} \text{LHS}^2 &= (z_1 + z_2) \overline{z_1 + z_2} \\ \text{RHS}^2 &= |z_1|^2 + 2|z_1||z_2| + |z_2|^2 \end{align*}\]
Compare “cross terms”: \[\begin{align*} & z_1\overline{z_2} + z_2 \overline{z_1} \leq 2 |z_1| |z_2| \\ & \iff \frac{1}{2} (z_1 \overline{z_2} + \overline{(z_1 \overline{z_2})}) \leq |z_1| |\overline{z_2}| \\ & \iff \operatorname{Re}(z_1 \overline{z_2}) \leq |z_1 \overline{z_2}| \end{align*}\]
An alternative form of the triangle inequality: replace \(z_2\) by \(z_2 - z_1\) and rearrange to get \[\begin{align*} | z_2 - z_1 | &\geq |z_2| - |z_1| \\ \text{or} &\geq |z_1| - |z_2| \\ \text{So } |z_2 - z_1| &\geq \left| |z_2| - |z_1| \right| \end{align*}\]
- i.e. moduli multiply and args add
Proposition 1.2 \[\begin{align*} &z_1 = r_1 (\cos \theta_1 + i \sin \theta_1),\ z_2 = r_2 (\cos \theta_2 + i \sin \theta_2) \\ &\implies z_1 z_2 = r_1 r_2 (\cos (\theta_1 + \theta_2) + i \sin (\theta_1 + \theta_2)) \end{align*}\]
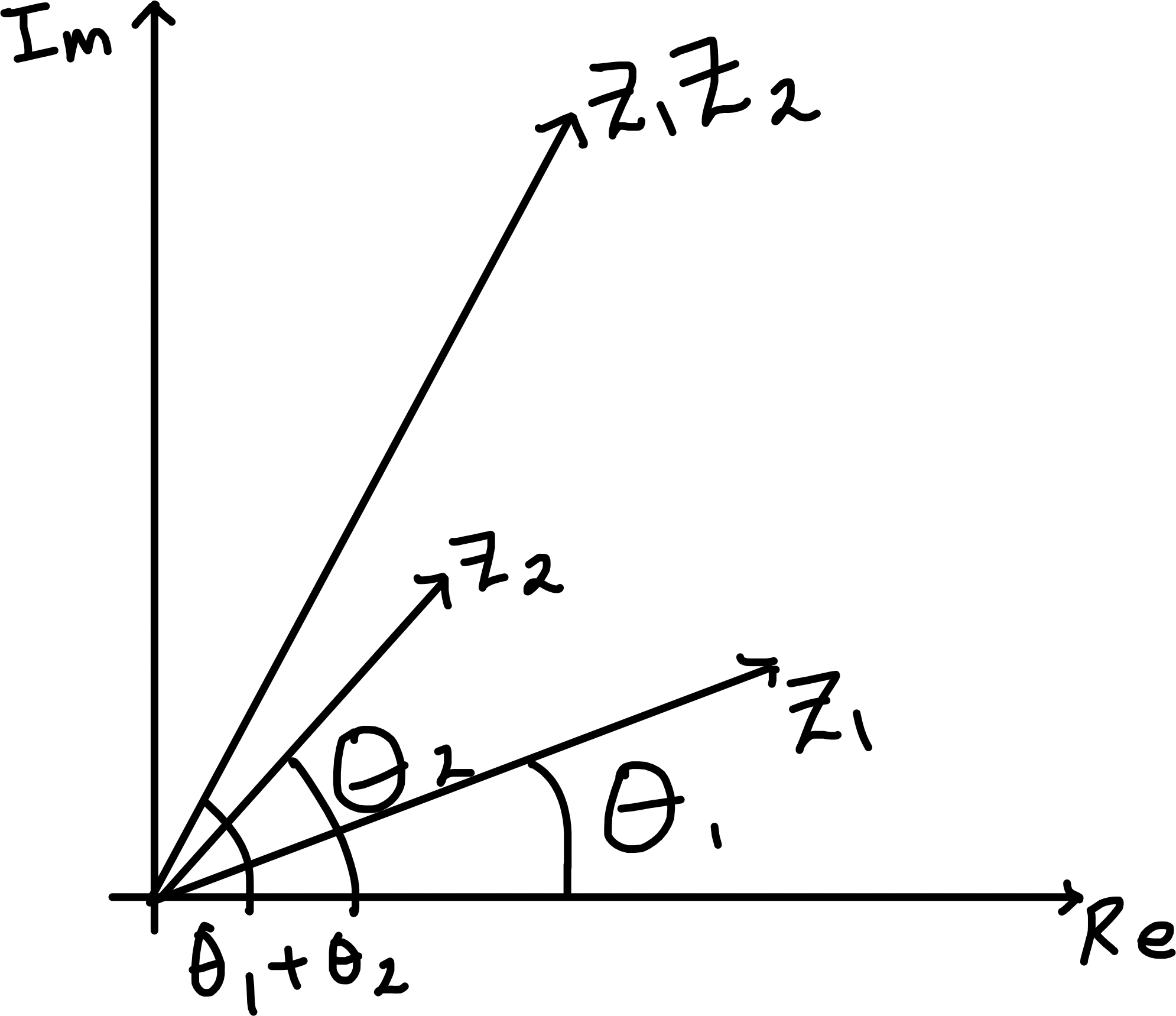
Proof. Direct check: calculate \(z_1 z_2\) and use standard trig formulas.
Theorem 1.1 (De Moivre's Theorem) \[\begin{align*} (\cos \theta + i \sin \theta)^n = \cos n \theta + i \sin n \theta,\ \text{ for } n \in \mathbb{Z} \end{align*}\] Note for \(z \neq 0\), \(z^0 = 1\) and \(z^{-n} = (z^{-1})^n\) for \(n > 0\).
Proof. Use 1.2 and induction
1.3 Exponential and Trigonometric Functions
Define \(\exp, \cos, \sin\) as functions on \(\mathbb{C}\) by \[\begin{align*} \exp(z) &= e^z = \sum_{n=0}^{\infty} \frac{1}{n!} z^n \\ \cos(z) &= \frac{1}{2} (e^{iz} + e^{-iz}) \\ &= 1 - \frac{1}{2!}z^2 + \frac{1}{4!}z^4 \ldots \\ \sin(z) &= \frac{1}{2i} (e^{iz} - e^{-iz}) \\ &= z - \frac{1}{3!}z^{3} + \frac{1}{5!}z^5 + \ldots \end{align*}\]
These series converge \(\forall \; z \in \mathbb{C}\) and such series can be multiplied, rearranged and differentiated. Furthermore \(e^{z}e^{w} = e^{z + w}\) and from this we can see \(e^{0} = 1\) and \((e^{z})^{n} = e^{nz}\) for \(n \in \mathbb{Z}\). For the positive integers this is trivial and for the negative integers we can know that \(e^z e^{-z} = 1\) so \(e^{-z} = (e^{z})^{-1}\).
Lemma 1.1 For \(z = x + iy\):
- \(e^z = e^x ( \cos y + i \sin y)\)
- \(\exp\) on \(\mathbb{C}\) takes all complex values except \(0\).
- \(e^z = 1 \iff z = 2n \pi i,\ n \in \mathbb{Z}\)
Proof. i. \(e^{x + iy} = e^x e^{iy}\) but \(e^{iy} = \cos y + i \sin y\)
\(|e^z| = e^x\), so \(|e^z|\) take all real values \(> 0\). \(\arg{e^z} = y\) taking all possible values.
\[\begin{align*} e^z = 1 &\iff e^x = 1, \cos y = 1, \sin y = 0 \\ &\iff x = 0, y = 2 \pi n \end{align*}\]
Returning to polar form 1.2, this can be written \(z = r ( \cos \theta + i \sin \theta) = re^{i \theta}\) for \(r = |z|\) and \(\theta = \arg z\). De Moivre’s Theorem 1.1 now follows from \((e^{i \theta})^n = e^{i n \theta}\).
1.3.1 Roots of units
\(z\) is an Nth root of unity if \(z^N = 1\). To find all solutions: \[\begin{align*} && z &= r e^{i \theta} \text{ satisfying } z^N = 1 \\ &\iff & r^N e^{i N \theta} &= 1 \\ &\iff & r^N &= 1 \text{ and } N \theta = 2n \pi,\ n \in \mathbb{Z} \end{align*}\]
This gives N distinct solutions. \[\begin{align*} z &= e^{2 \pi i n/N} \\ &= \cos \frac{2\pi n}{N} + i \sin \frac{2 \pi n}{N} \\ \text{The only distinct cases are when } n &= 0, 1, 2 \ldots N - 1 \text{ due to periodicity} \\ &= \omega^n, \text{ where } \omega = e^{2 \pi i / N} \end{align*}\] These solutions lie at vertices of a regular N-gon.
Figure 1.1: N = 6
1.4 Transformations; lines and circles
Consider the following transformations on \(\mathbb{C}\) (maps \(\mathbb{C} \to \mathbb{C}\)) \[\begin{align*} z &\mapsto z + a & &(\text{translation}) \\ z &\mapsto \lambda z & &(\text{scaling by } \lambda \in \mathbb{R}) \\ z &\mapsto e^{i \alpha} z & &(\text{rotation by } \alpha \in \mathbb{R}) \\ z &\mapsto \overline{z} & &(\text{reflection in the real axis}) \\ z &\mapsto \frac{1}{z} & &(\text{inversion}) \end{align*}\]
Consider a general point on a line in \(\mathbb{C}\) through \(z_0\) and parallel to \(w \neq 0\) (fixed \(z_0, w \in \mathbb{C}\)):
\[\begin{align*} z = z_0 + \lambda w,\ \lambda \in \mathbb{R} \end{align*}\]
To eliminate \(\lambda\), take the conjugate to get \(\overline{z} = \overline{z_0} + \lambda \overline{w}\) and equate \(\lambda\) to get \(\overline{w}z - w\overline{z} = \overline{w} z_0 - w \overline{z_0}\).
Consider a general point on a circle in \(\mathbb{C}\) with centre \(c \in \mathbb{C}\) and radius \(\rho \in \mathbb{R}^{++}\). \[\begin{align*} z = c + \rho &e^{i \alpha}, \text{ for any } \alpha \in \mathbb{R} \\ \text{Equivalently} \\ |z - c| &= \rho \\ \text{or } \\ |z - c|^2 &= \rho^2 \\ |z|^2 - \overline{c}z - c \overline{z} &= \rho^2 - |c|^2 \end{align*}\]
Möbius transformations are generated by translations, scalings, rotations and inversion. They can be viewed as acting on \(\mathbb{C}_\infty = \mathbb{C} \cup \{ \infty \}\) - geometrically a sphere (see IA Groups). We add \(\infty\) to deal with \(0^{-1}\)?
1.5 Logarithms and Complex Powers
Define \(w = \log z,\ z \in \mathbb{C},\ z \neq 0\) by \(e^w = \exp w = z\) i.e. \(\log\) is the inverse of \(\exp\), but \(\exp\) is many-to-one (\(e^z = e^{z + 2n \pi i}\)) and so \(\log\) is multi-valued. \[\begin{align*} z &= r e^{i \theta} \\ &= e^{\log r} e^{i \theta} \\ &= e^{\log r + i \theta} \\ \implies \log z &= \log r + i \theta \\ &= \log |z| + i \arg z \end{align*}\] Multiple values of \(\arg\) and \(\log\) are related: \[\begin{align*} \theta &\to \theta + 2n \pi,\ n \in \mathbb{Z} \\ \log z &\to \log z + 2n \pi i,\ n \in \mathbb{Z} \end{align*}\] To make them single valued we can restrict e.g. \(0 \leq \theta < 2 \pi\) or \(-\pi < \theta \leq \pi\) (principal value).
Example 1.2 \[\begin{align*} z &= -3i = 3 (-i) \\ &= e^{\log 3}e^{-i \pi / 2 + 2n \pi i} \\ &= e^{\log 3 -i \pi / 2 + 2n \pi i} \\ \log z &= \log 3 -i \pi / 2 + 2n \pi i \\ \arg z &= 3 \pi / 2 \\ &\text{or } - \pi / 2 \text{ with the restrictions above} \end{align*}\]
Define complex powers by \[\begin{align*} z^\alpha = e^{\alpha \log z},\ z \in \mathbb{C},\ z \neq 0,\ \alpha \in \mathbb{C} \end{align*}\] This is multi-valued in general under the change \(\arg z \to \arg z + 2n\pi\) \[\begin{align*} z^\alpha \to z^\alpha e^{2 \pi i n \alpha} \end{align*}\]
- If \(\alpha = p \in \mathbb{Z}\) then \(z^\alpha = z^p\) is unique
- If \(\alpha = \frac{p}{q} \in \mathbb{Q}\) then \(z^\alpha = z^{\frac{p}{q}}\) takes finitely many values.
But in general we have infinitely many values
Example 1.3 \[\begin{align*} (1 + i)^{\frac{1}{2}}: 1 + i &= \sqrt{2} e^{i \pi /4} \\ &= e^{\frac{1}{2} \log 2 + i \pi /4} \\ \log(1 + i) &= \frac{1}{2} \log 2 + i \pi / 4 + 2 n \pi i \\ \implies (1 + i)^{\frac{1}{2}} &= e^{\frac{1}{2} \log (1 + i)} \\ &= e^{\frac{1}{4} \log 2 + i \pi / 8 + n \pi i} \\ &= 2^{\frac{1}{4}} e^{i \pi / 8} (-1)^n \end{align*}\]
Example 1.4 \[\begin{align*} (-3i)^i &= e^{i \log (-3i)} \\ &= e^{i (\log 3 - i \pi /2 + 2 n \pi i)} \\ &= e^{i \log 3} e^{\pi /2 - 2 n \pi},\ n \in \mathbb{Z} \end{align*}\]