4 Matrices and Linear Maps

4.1 Introduction

4.1.1 Definitions

Definition 4.1 A linear map or linear transformation is a function \[\begin{align*} T : V \to W \end{align*}\] between vector spaces $V\ (\dim n)$ and $W\ (\dim m)$ such that \[\begin{align*} T(\lambda \underline{x} + \mu \underline{y}) &= \lambda T(\underline{x}) + \mu T(\underline{y}) \\ \forall \; \underline{x}, \underline{y} \in V \\ \forall \; \lambda, \mu \in \mathbb{R} \text{ or } \mathbb{C} \end{align*}\] for $V, W$ both real or complex vector spaces.⁶

Note: a linear map is completely determined by its action on a basis $\{ \underline{e}_1, \dots, \underline{e}_n \}$ for $V$, since \[\begin{align*} T\left( \sum_i x_i \underline{e}_i \right) = \sum_i x_i T(\underline{e}_i) \end{align*}\]

$\underline{x}' = T(\underline{x}) \in W$ is the image of $\underline{x} \in V$ under T.
$\operatorname{Im}(T) = \{ \underline{x}' \in W: \underline{x}' = T(\underline{x}) \text{ for some } \underline{x} \in V \}$ is the image of $T$.
$\ker(T) = \{ \underline{x} \in V: \underline{x}' = T(\underline{x}) = \underline{0} \}$ is the kernel of $T$.

Lemma 4.1 $\ker(T)$ is a subspace of $V$ and $\operatorname{Im}(T)$ is a subspace of $W$.

Proof. $\underline{x}, \underline{y} \in \ker(T) \implies T(\lambda \underline{x} + \mu \underline{y}) = \lambda T(\underline{x}) + \mu T(\underline{y}) = \underline{0}$ and $\underline{0} \in \ker(T)$, so results follows.

Also $\underline{0} \in \operatorname{Im}(T)$ and $\underline{x}', \underline{y}' \in \operatorname{Im}(T)$ then $T(\lambda \underline{x} + \mu \underline{y}) = \lambda T(\underline{x}) + \mu T(\underline{y}) = \lambda \underline{x}' + \mu \underline{y}' \in \operatorname{Im}(T)$ for some $\underline{x}, \underline{y} \in V$.

Example 4.1 Zero linear map $T : V \to W$ is given by $T(\underline{x}) = \underline{0} \ \forall \; \underline{x} \in V$. $\operatorname{Im}(T) = \{ \underline{0} \}$ and $\ker(T) = V$

Example 4.2 For $V = W$, the identity linear map $T: V \to V$ is given by $T(\underline{x}) = \underline{x} \; \forall \; x \in V$. $\operatorname{Im}(T) = V$ and $\ker(T) = \{ \underline{0} \}$

Example 4.3 $V = W = \mathbb{R}^3$, $\underline{x}' = T(\underline{x})$ given by \[\begin{align*} x_1' &= 3 x_1 + x_2 + 5 x_3 \\ x_2' &= - x_1 - 2 x_3 \\ x_3' &= 2 x_1 + x_2 + 3 x_3 \\ \ker(T) &= \left\{ \lambda \begin{pmatrix}2 \\-1 \\-1\end{pmatrix} \right\} \hspace{0.5cm} (\dim 1) \\ \operatorname{Im}(T) &= \left\{ \lambda \begin{pmatrix}3 \\-1 \\2\end{pmatrix} + \mu \begin{pmatrix}1 \\0 \\1\end{pmatrix} \right\} \hspace{0.5cm} (\dim 2) \end{align*}\]

4.1.2 Rank and Nullity

$\dim \operatorname{Im}(T)$ is the rank of $T$ ($\leq n$).
$\dim \ker(T)$ is the nullity of $T$ ($\leq n$).

Theorem 4.1 (rank-nullity) For $T : V \to W$ a linear map, 4.1 \[\begin{align*} \operatorname{rank}(T) + \operatorname{null}(T) &= n = \dim V \end{align*}\]

Example 4.4 same as those in Definitions

$\operatorname{rank}(T) + \operatorname{null}(T) = 0 + n = n$
$\operatorname{rank}(T) + \operatorname{null}(T) = n + 0 = n$
$\operatorname{rank}(T) + \operatorname{null}(T) = 2 + 1 = 3$

Non-examinable

Proof. Let $\underline{e}_1, \dots, \underline{e}_k$ be a basis for $\ker(T)$ so $T(\underline{e}_i) = 0$ for $i = 1, \dots, k$.
Extend by $\underline{e}_{k + 1}, \dots, \underline{e}_n$ to get a basis for $V$. Claim \[\begin{align*} \mathcal{B} &= \{ T(\underline{e}_{k + 1}), \dots, T(\underline{e}_n) \} \end{align*}\] is the basis for $\operatorname{Im}(T)$. The result then follows since $\operatorname{null}(T) = k$ and $\operatorname{rank}(T) = n - k$, implying $\operatorname{null}(T) + \operatorname{rank}(T) = n$.

To check claim:
$\mathcal{B}$ spans $\operatorname{Im}(T)$ since $\underline{x} = \sum_{i=1}^{n} x_i \underline{e}_i$ \[\begin{align*} \implies T(\underline{x}) = \sum_{i=1}^{n} x_i T(\underline{e}_i) = \sum_{i = k + 1}^{n} x_i T(\underline{e}_i) \end{align*}\] $\mathcal{B}$ is linearly independent since \[\begin{align*} \sum_{i=k+1}^{n} \lambda_i T(\underline{e}_i) &= \underline{0} \\ \implies T(\sum_{i=k+1}^{n} \lambda_i \underline{e}_i) &= \underline{0} \\ \implies \sum_{i=k+1}^{n} \lambda_i \underline{e}_i &\in \ker(T) \\ \implies \sum_{i=k+1}^{n} \lambda_i \underline{e}_i &= \sum_{i=1}^{k} \mu_i \underline{e}_i \end{align*}\] But $\underline{e}_1, \dots, \underline{e}_n$ are linearly independent in $V$ \[\begin{align*} \implies \lambda_i &= 0 \\ \mu_i &= 0 \end{align*}\]

4.2 Geometrical Examples

4.2.1 Rotations

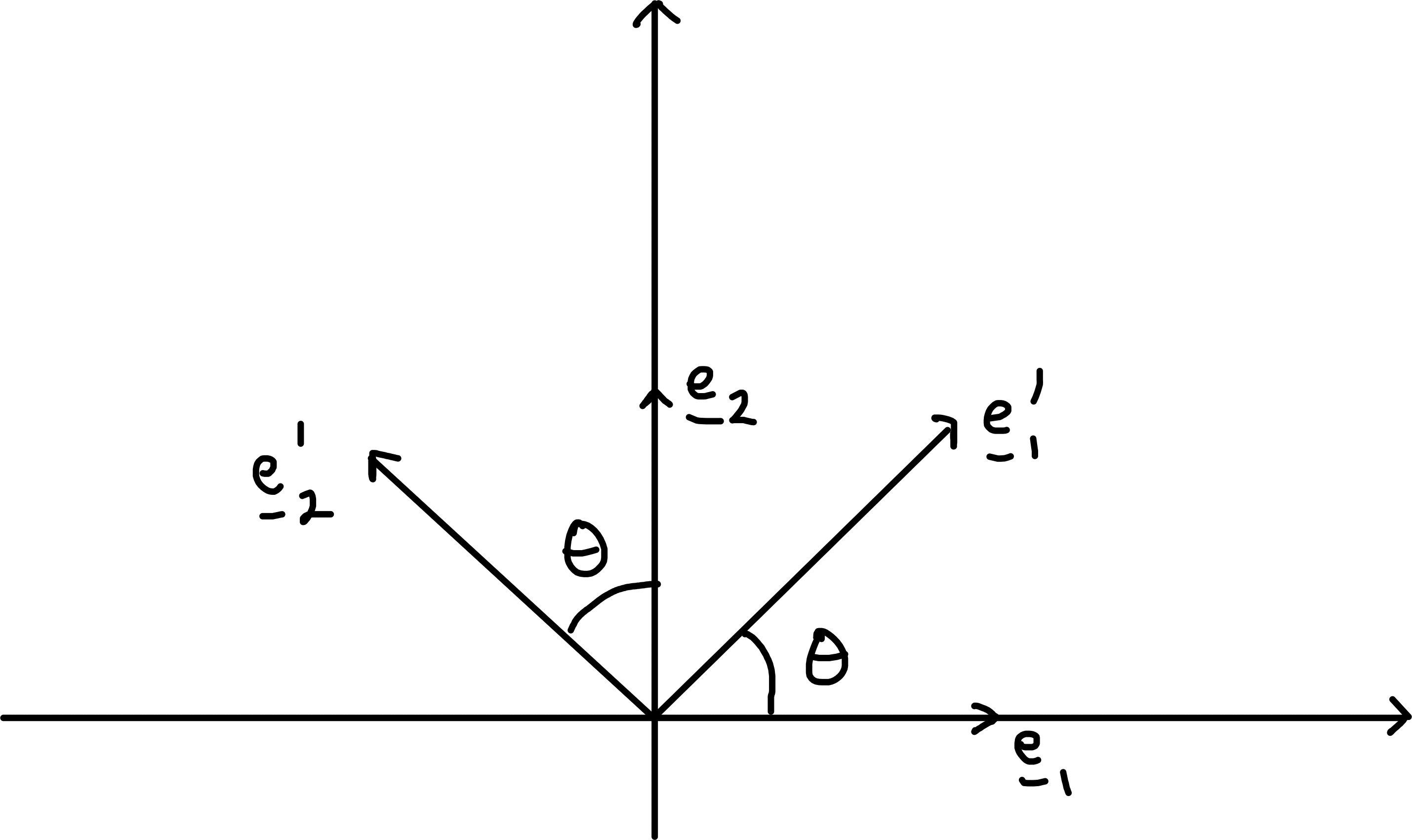
In $\mathbb{R}^2$, a rotation about $\underline{0}$ through angle $\theta$ is defined by \[\begin{align*} \underline{e}_1 &\mapsto \underline{e}_1' = \ \; (\cos \theta) \underline{e}_1 + (\sin \theta) \underline{e}_2 \\ \underline{e}_2 &\mapsto \underline{e}_2' = -(\sin \theta) \underline{e}_1 + (\cos \theta) \underline{e}_2 \end{align*}\]

In $\mathbb{R}^3$, rotation about axis given by $\underline{e}_3$ is defined as above, with \[\begin{align*} \underline{e}_3 \mapsto \underline{e}_3' = \underline{e}_3 \end{align*}\]

Now consider rotation about any axis $\underline{n}$ (a unit vector). Given $\underline{x}$, resolve $\parallel$ and $\perp$ to $\underline{n}$: \[\begin{align*} \underline{x} &= \underline{x}_\parallel + \underline{x}_\perp \hspace{0.5cm} \text{with } \underline{x}_\parallel = (\underline{x} \cdot \underline{n}) \underline{n} \ (\implies \underline{n} \cdot \underline{x}_\perp = \underline{0}) \\ \text{Under rotation} \\ \underline{x}_\parallel &\mapsto \underline{x}_\parallel' = \underline{x}_\parallel \\ \underline{x}_\perp &\mapsto \underline{x}_\perp' = (\cos \theta) \underline{x}_\perp + (\sin \theta) \underline{n} \wedge \underline{x}, \end{align*}\] by considering plane $\perp \underline{n}$, comparing to rotation in $\mathbb{R}^2$ and noting that $|\underline{x}_\perp| = | \underline{n} \wedge \underline{x} |$.

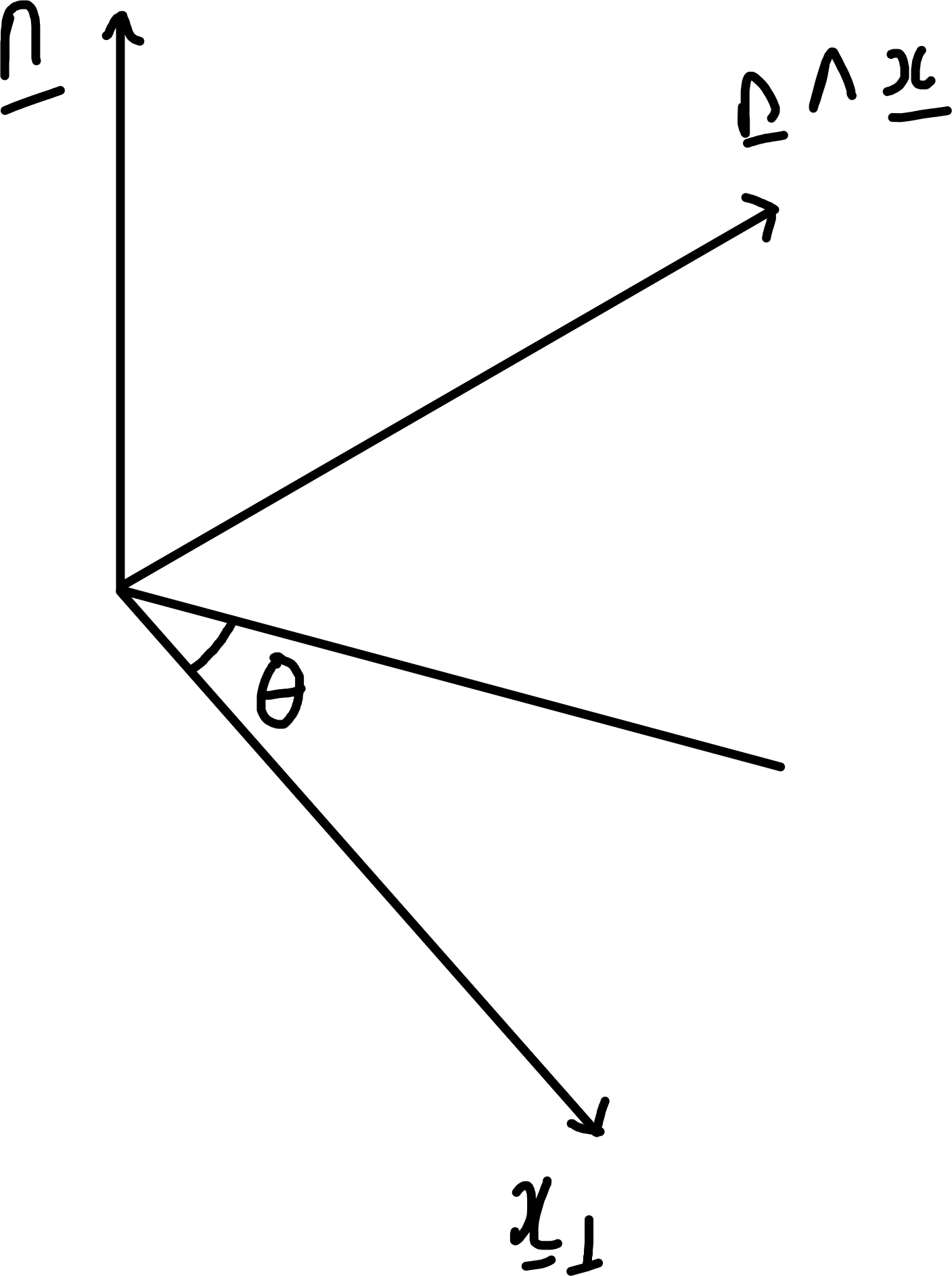
\[\begin{align*} \underline{x} \mapsto \underline{x}' &= \underline{x}_\parallel' + \underline{x}_\perp' \\ &= (\cos \theta) \underline{x} + (1 - \cos \theta) (\underline{n} \cdot \underline{x}) \underline{n} + \sin \theta \underline{n} \wedge \underline{x}. \end{align*}\]

4.2.2 Reflections

Consider a reflection in a plane in $\mathbb{R}^3$ (or line in $\mathbb{R}^2$) through $\underline{0}$ with unit normal $\underline{n}$.
Given $\underline{x}$, resolve $\parallel$ and $\perp$ to $\underline{n}$: \[\begin{align*} \underline{x}_\parallel &\mapsto \underline{x}_\parallel' = -\underline{x}_\parallel \\ \underline{x}_\perp &\mapsto \underline{x}_\perp' = \underline{x}_\perp \end{align*}\]

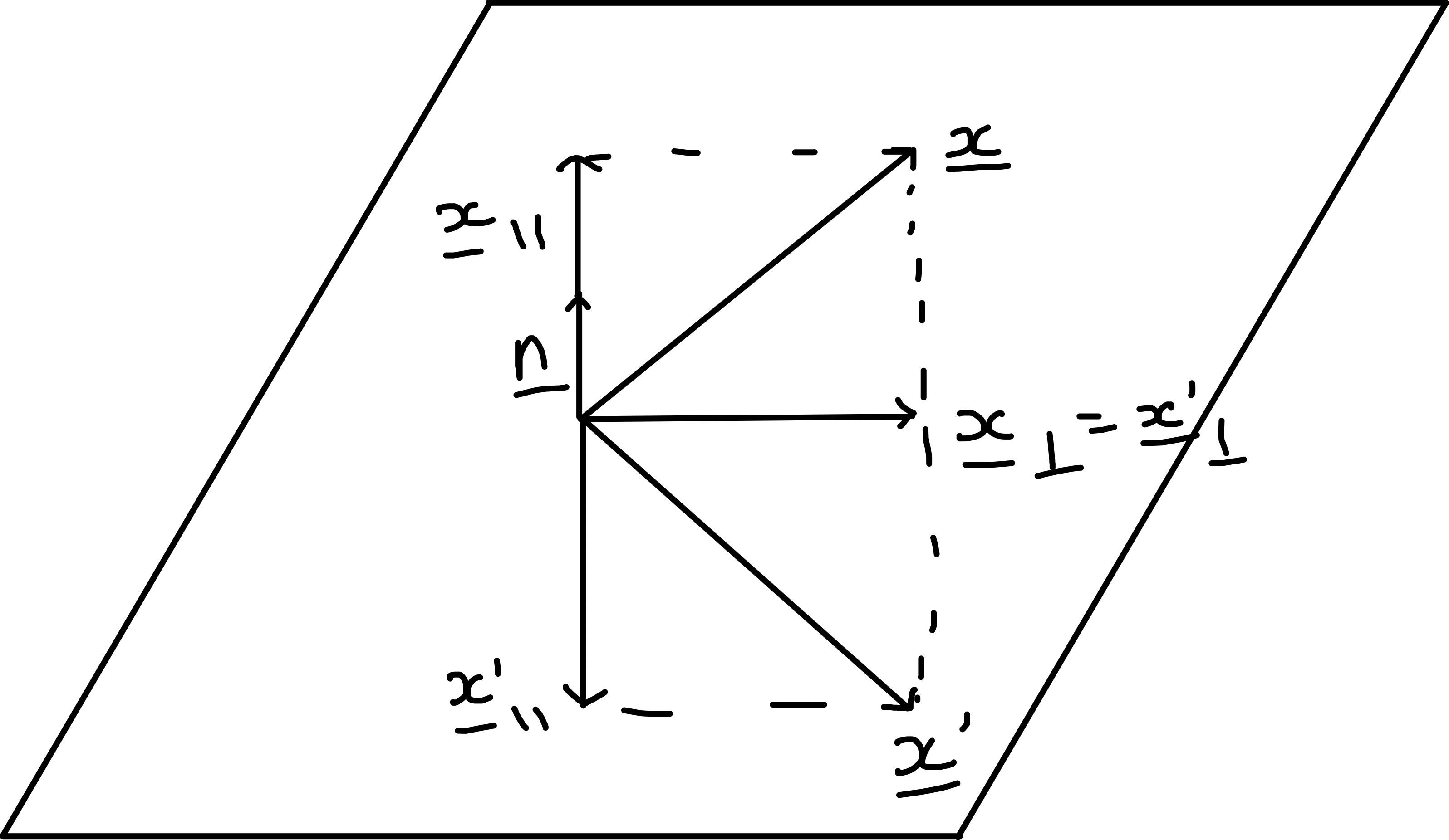
\[\begin{align*} \underline{x} &\mapsto \underline{x}' = \underline{x} - 2 (\underline{x} \cdot \underline{n}) \underline{n} \end{align*}\]

4.2.3 Dilations

A dilation by scale factors $\alpha, \beta, \gamma$ (real, $> 0$) along axes $\underline{e}_1, \underline{e}_2, \underline{e}_3$ in $\mathbb{R}^3$ is defined by \[\begin{align*} \underline{x} &= x_1 \underline{e}_1 + x_2 \underline{e}_2 + x_3 \underline{e}_3 \\ \mapsto \underline{x}' &= \alpha x_1 \underline{e}_1 + \beta x_2 \underline{e}_2 + \gamma x_3 \underline{e}_3. \end{align*}\]

A dilation maps a unit cube to a cuboid.

4.2.4 Shears

Given $\underline{a}, \underline{b}$ orthogonal unit vectors define a shear with parameter $\lambda$ by \[\begin{align*} \underline{x} &\mapsto \underline{x}' = \underline{x} + \lambda (\underline{x} \cdot \underline{b}) \underline{a} \end{align*}\]

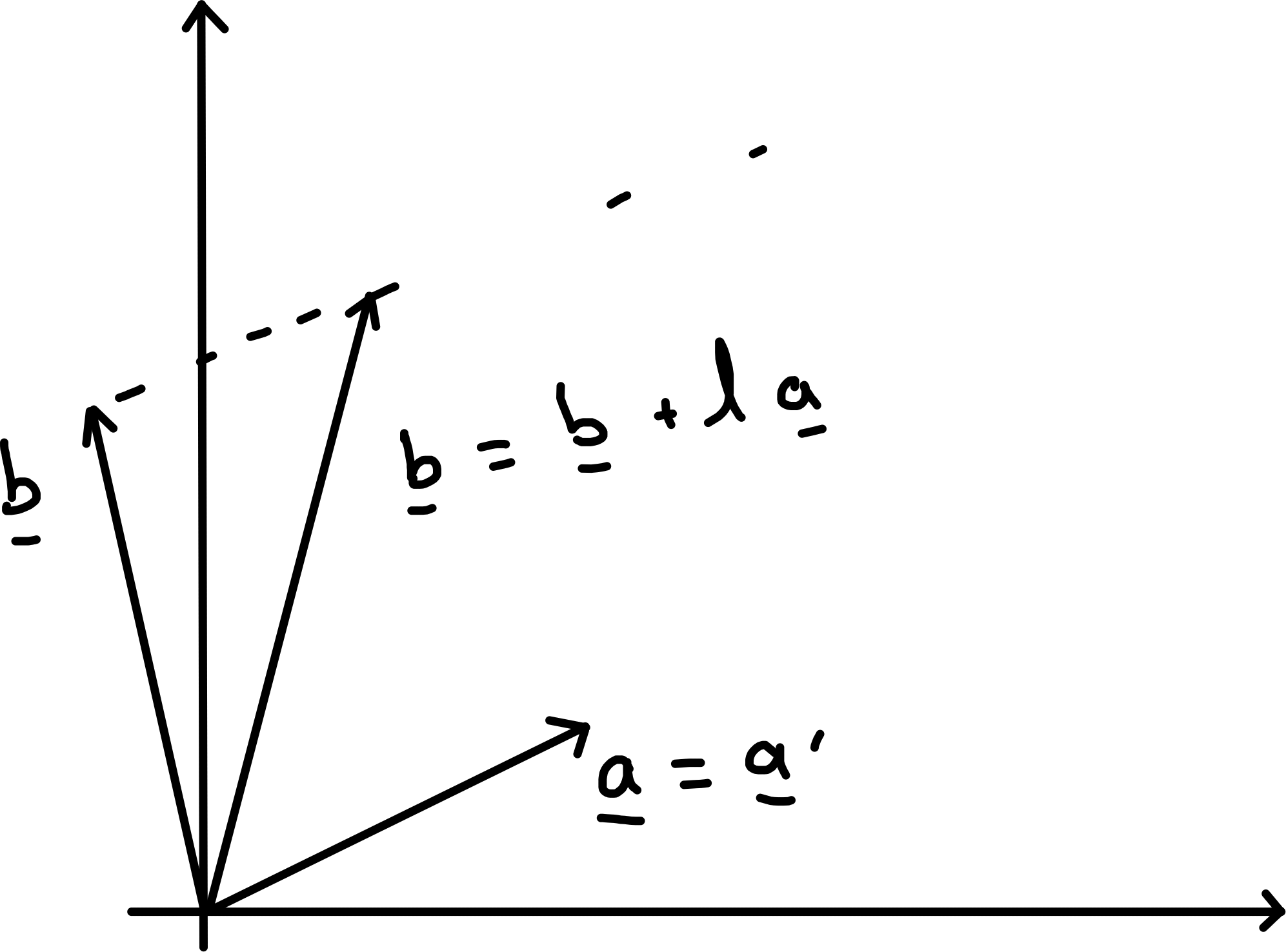
Definition applies in $\mathbb{R}^n$ and $\underline{u}' = u$ for any vector $\underline{u} \perp \underline{b}$.

4.3 Matrices as Linear Maps $\mathbb{R}^n \to \mathbb{R}^m$

4.3.1 Definitions

Consider a linear map $T : \mathbb{R}^n \to \mathbb{R}^m$ and standard bases $\{ \underline{e}_i \}$ and $\{ \underline{f}_a \}$ respectively.
Let $\underline{x}' = T(\underline{x})$ with \[\begin{align*} \underline{x} = \sum_i x_i \underline{e}_i = \begin{pmatrix}x_1 \\ \vdots \\ x_n\end{pmatrix},\ \underline{x}' = \sum_a x_a' \underline{f}_a = \begin{pmatrix}x_1' \\ \vdots \\ x_m'\end{pmatrix} \end{align*}\] Linearity implies $T$ is determined by $T(\underline{e}_i) = \underline{e}_i' = \underline{C}_i \in \mathbb{R}^m \ (i = 1, \dots, n)$; take these as columns of a $m \times n$ array or matrix $M$ with rows \[\begin{align*} \underline{R}_a \in \mathbb{R}^n \ (a = 1, \dots, m). \end{align*}\] $M$ has entries $M_{ai} \in \mathbb{R}$ where $a$ labels rows and $i$ labels columns.

\[\begin{align*} \begin{pmatrix} \uparrow & & \uparrow \\ \underline{C}_1 & \dots & \underline{C}_n \\ \downarrow & & \downarrow \end{pmatrix} = M = \begin{pmatrix} \leftarrow & \underline{R}_1 & \rightarrow \\ & \vdots & \\ \leftarrow & \underline{R}_m & \rightarrow \end{pmatrix} \end{align*}\]

$(\underline{C}_i)_a = M_{ai} = (\underline{R}_a)_i$.

Action of $T$ is given by matrix $M$ multiplying vector $\underline{x}$,

$\underline{x}' = M \underline{x}$ defined by $x_a' = M_{ai} x_i$ ($\sum$ convention).

This follows from definitions above since \[\begin{align*} \underline{x}' &= T\left( \sum_i x_i \underline{e}_i \right) = \sum_i x_i \underline{C}_i \\ \implies (\underline{x}')_a &= \sum_i x_i (\underline{C}_i)_a \\ &= \sum_i M_{ai} x_i \\ &= \sum_i (\underline{R}_a) x_i \\ &= \underline{R}_a \cdot x \end{align*}\]

Now regard properties of $T$ as properties of $M$.
$\operatorname{Im}(T) = \operatorname{Im}(M) = \operatorname{span} \{ \underline{C}_1, \dots, \underline{C}_n \}$, the image of M (or T) is the span of the columns.
$\ker(T) = \ker(M) = \{\underline{x} : \underline{R}_a \cdot \underline{x} = 0 \; \forall \; a \}$, kernel of M is subspace $\perp$ all rows.

4.3.2 Examples

Refer to Examples 4.1, 4.2, 4.3, 4.4.

Example 4.5 Zero map $\mathbb{R}^n \to \mathbb{R}^m$ corresponds to zero matrix $M = 0$ with $M_{ai} = 0$.

Example 4.6 Identity map $\mathbb{R}^n \to \mathbb{R}^n$ corresponds to identity matrix \[\begin{align*} M = I = \begin{pmatrix} 1 & & & \smash{\huge 0} \\ & 1 & & \\ & & \ddots & \\ \huge 0 & & & 1 \end{pmatrix} \end{align*}\] with $I_{ij} = \delta_{ij}$.

Example 4.7 $\mathbb{R}^3 \to \mathbb{R}^3$, $\underline{x}' = T(\underline{x}) = M \underline{x}$ with \[\begin{align*} M &= \begin{pmatrix} 3 & 1 & 5 \\ -1 & 0 & -2 \\ 2 & 1 & 3 \end{pmatrix}, \underline{C}_1 = \begin{pmatrix}3 \\-1 \\2\end{pmatrix}, \underline{C}_2 = \begin{pmatrix}1 \\0 \\1\end{pmatrix}, \underline{C}_3 = \begin{pmatrix}5 \\-2 \\3\end{pmatrix} \\ \operatorname{T} &= \operatorname{M} \\ &= \operatorname{span} \{ \underline{C}_1, \underline{C}_2, \underline{C}_3 \} \\ &= \operatorname{span} \{ \underline{C}_1, \underline{C}_2 \} \text{ since } \underline{C}_3 = 2 \underline{C}_1 - \underline{C}_2 \\ \underline{R}_1 &= \begin{pmatrix}3 & 1 & 5\end{pmatrix} \\ \underline{R}_2 &= \begin{pmatrix}-1 & 0 & 2\end{pmatrix} \\ \underline{R}_3 &= \begin{pmatrix}2 & 1 & 3\end{pmatrix} \\ \underline{R}_2 \wedge \underline{R}_3 &= \begin{pmatrix}2 & -1 & -1\end{pmatrix} \\ &= \underline{u}, \text{ say } \perp \text{ all rows (in fact)} \\ \ker (T) &= \ker (M) = \{ \lambda \underline{u} \} \end{align*}\]

Example 4.8 Rotation through $\theta$ about $\underline{0}$ in $\mathbb{R}^2$ \[\begin{align*} \underline{e}_1 &= \begin{pmatrix}1 \\0\end{pmatrix} \mapsto \begin{pmatrix} \cos \theta \\ \sin \theta\end{pmatrix} = \underline{C}_1 \\ \underline{e}_2 &= \begin{pmatrix}0 \\1\end{pmatrix} \mapsto \begin{pmatrix}- \sin \theta \\ \cos \theta\end{pmatrix} = \underline{C}_2 \\ \implies M &= \begin{pmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}. \end{align*}\]

Example 4.9 Dilation $\underline{x}' = M \underline{x}$ with scale factors $\alpha, \beta, \gamma$ along axes in $\mathbb{R}^3$. \[\begin{align*} M = \begin{pmatrix} \alpha & 0 & 0 \\ 0 & \beta & 0 \\ 0 & 0 & \gamma \end{pmatrix}. \end{align*}\]

Example 4.10 Reflection in plane $\perp \underline{n}$ (a unit vector). \[\begin{align*} \underline{x}' &= H \underline{x} = \underline{x} - 2 (\underline{x} \cdot \underline{n}) \underline{n} \\ x_i' &= x_i - 2 x_j n_j n_i \\ &= (\delta_{ij} - 2 n_j n_i) x_j \\ H_{ij} &= \delta_{ij} - 2 n_j n_i \\ \text{e.g. } \underline{n} &= \frac{1}{\sqrt{3}} \begin{pmatrix}1 \\1 \\1\end{pmatrix},\ n_i n_j = \frac{1}{3} \quad \forall \; i, j \\ H &= \frac{1}{3} \begin{pmatrix} 1 & -2 & -2 \\ -2 & 1 & -2 \\ -2 & -2 & 1 \end{pmatrix} \end{align*}\]

Example 4.11 Shear \[\begin{align*} \underline{x}' &= S \underline{x} = \underline{x} + \lambda (\underline{b} \cdot \underline{x})\underline{a} \\ x_i' &= S_{ij} x_j \\ \text{with } S_{ij} &= \delta_{ij} + \lambda a_i b_j \end{align*}\] e.g. in $\mathbb{R}^2$ with $\underline{a} = \begin{pmatrix}1 \\0\end{pmatrix}$ and $\underline{b} = \begin{pmatrix}0 \\1\end{pmatrix}$, \[\begin{align*} S = \begin{pmatrix} 1 & \lambda \\ 0 & 1 \end{pmatrix}. \end{align*}\]

Example 4.12 Rotation in $\mathbb{R}^3$ with axis $\underline{n}$ and angle $\theta$, \[\begin{align*} \underline{x}' &= R \underline{x} \hspace{1cm} x_i' = R_{ij} x_j \\ \text{where } R_{ij} &= \delta_{ij} \cos \theta + (1 - \cos \theta) n_i n_j - (\sin \theta) \epsilon_{ijk} n_k \end{align*}\] (see Example Sheet 2).

4.3.3 Isometries, area and determinants in $\mathbb{R}^2$

Consider a linear map $\mathbb{R}^2 \to \mathbb{R}^2$ given by $2 \times 2$ matrix $M$: \[\begin{align*} \underline{x} \mapsto \underline{x}' = M \underline{x} \end{align*}\]

When is $M$ an isometry, preserving lengths $|\underline{x}'| = |\underline{x}|$?

This is equivalent to preserving inner products $\underline{x}' \cdot \underline{y}' = \underline{x} \cdot \underline{y}$ [since $\underline{x} \cdot \underline{y} = \frac{1}{2} ( |\underline{x} + \underline{y}|^2 - |\underline{x}|^2 - |\underline{y}|^2)$].
Necessary conditions are \[\begin{align*} M \begin{pmatrix} 1 \\ 0 \end{pmatrix} &= \begin{pmatrix}\cos \theta \\\sin \theta\end{pmatrix} \text{ for some $\theta$; most general unit vector in $\mathbb{R}^2$} \\ M \begin{pmatrix}0 \\1\end{pmatrix} &= \pm \begin{pmatrix}- \sin \theta \\ \cos \theta\end{pmatrix} \text{ general unit vector $\perp M (1\ 0)^T$}. \end{align*}\] Simple to check that these conditions are also sufficient and have two cases \[\begin{align*} M = R = \begin{pmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}, \end{align*}\] a rotation, or \[\begin{align*} M = H = \begin{pmatrix} \cos \theta & \sin \theta \\ \sin \theta & - \cos \theta \end{pmatrix}, \end{align*}\] a reflection.

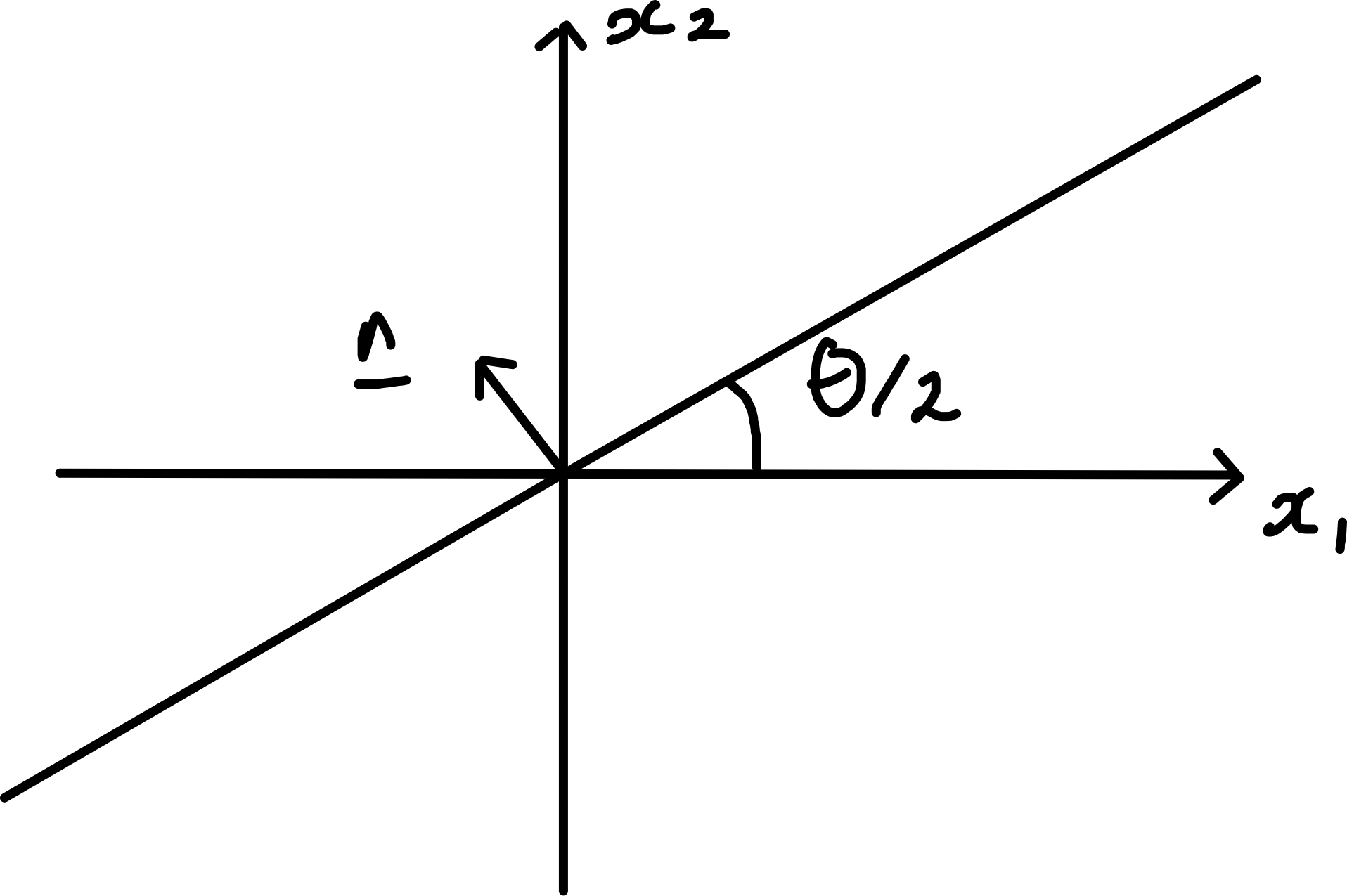
Compare with expression for reflection in 4.10

\[\begin{align*} H_{ij} &= \delta_{ij} - 2 n_i n_j \\ \text{and note for } \underline{n} &= \begin{pmatrix}n_1 \\n_2\end{pmatrix} = \begin{pmatrix} -\sin \frac{\theta}{2} \\ \cos \frac{\theta}{2}\end{pmatrix} \\ \text{we get } H &= \begin{pmatrix} 1 - 2 \sin^2 \frac{\theta}{2} & 2 \sin \frac{\theta}{2} \cos \frac{\theta}{2} \\ 2 \sin \frac{\theta}{2} \cos \frac{\theta}{2} & 1 - 2 \cos^2 \frac{\theta}{2} \end{pmatrix} \end{align*}\] agreeing with H above. This is reflection in a line in $\mathbb{R}^2$ as shown

How does $M$ change areas in $\mathbb{R}^2$ (in general)?

Consider unit square in $\mathbb{R}^2$, mapped to parallelogram as shown, with signed area $[M \underline{e}_1, M \underline{e}_1]$ “scalar cross product”.

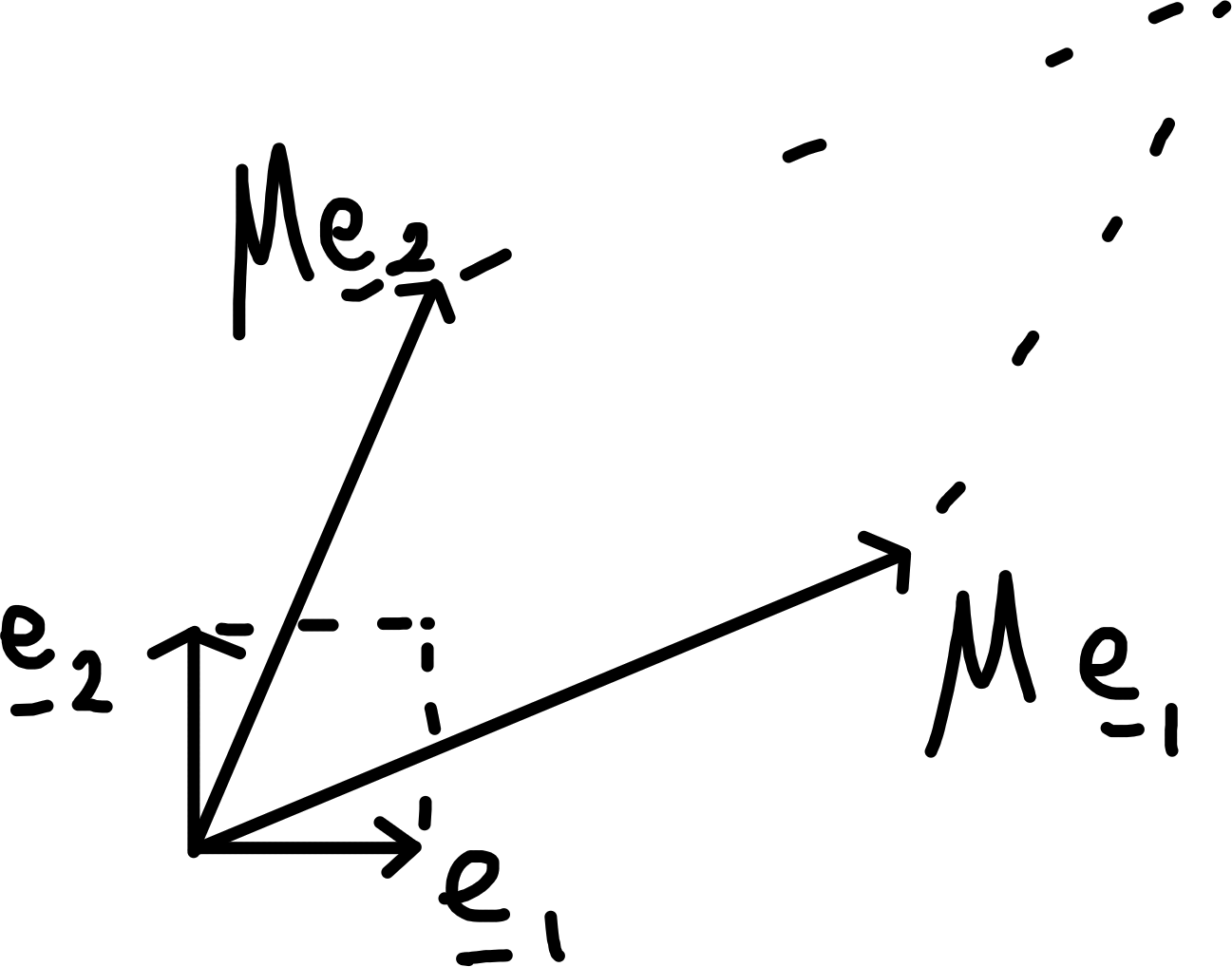
\[\begin{align*} \left[ \begin{pmatrix} M_{11} \\M_{21}\end{pmatrix}, \begin{pmatrix}M_{12} \\M_{22}\end{pmatrix} \right] &= M_{11} M_{22} - M_{12} M_{21} \\ &= \det M, \end{align*}\] the determinant of $2 \times 2$ matrix.

This is the factor (with a sign) by which areas are scaled under $M$.

Now compare with (i): \[\begin{align*} \det R = + 1,\ \det H = -1. \end{align*}\] In either case $| \det M | = + 1$. Consider shear $S = \begin{pmatrix}1 & \lambda \\0 & 1\end{pmatrix}$; this has $\det S = + 1$ but it does not preserve lengths.

4.4 Matrices for Linear Maps in General

Consider a linear map \[\begin{align*} T : V \to W \end{align*}\] between real or complex vector spaces of $\dim n, m$ respectively and choose bases $\{ \underline{e}_i \}$ with $i = 1, \dots, n$ for $V$ and $\{ \underline{f}_a \}$ with $a = 1, \dots, m$ for $W$.
The matrix $M$ for $T$ wrt the bases in an $m \times n$ array with entries $M_{ai} \in \mathbb{R}$ or $\mathbb{C}$. It is defined by \[\begin{align*} T(\underline{e}_i) &= \sum_a \underline{f}_a M_{ai} \text{ note index positions}. \end{align*}\] This is chose to ensure that $T(\underline{x}) = \underline{x}'$ where $\underline{x} = \sum_i x_i \underline{e}_i$ and $\underline{x}' = \sum_a x_a' \underline{f}_a$ iff $x_a' = \sum_i M_{ai} x_i$.
\[\begin{align*} \text{i.e. } \begin{pmatrix}x_1' \\ \vdots \\ x_m'\end{pmatrix} = \begin{pmatrix} M_{11} & \dots & M_{1n} \\ \vdots & & \vdots \\ M_{m1} & \dots & M_{mn} \end{pmatrix} \begin{pmatrix}x_1 \\ \vdots \\ x_n\end{pmatrix}. \end{align*}\]

Moral: given choice of bases $\{ \underline{e}_i \}$ and $\{ \underline{f}_a \}$
$V$ is identified with $\mathbb{R}^n$ (or $\mathbb{C}^n$)
$W$ is identified with $\mathbb{R}^m$ (or $\mathbb{C}^m$)
$T$ is identified with $m \times n$ matrix $M$.

Note: there are natural ways to combine linear maps.
If $S : V \to W$ is also linear, then so is $\alpha T + \beta S : V \to W$ defined by $(\alpha T + \beta S) (\underline{x}) = \alpha T(\underline{x}) + \beta S(\underline{x})$.
Or if $S : U \to V$ is also linear, then so is $T \circ S : U \to W$ (composition of maps).

4.5 Matrix Algebra

4.5.1 Linear Combinations

If $M$ and $N$ are $m \times n$ matrices then $\alpha M + \beta N$ is an $m \times n$ matrix defined by \[\begin{align*} (\alpha M + \beta N)_{ai} &= \alpha M_{ai} + \beta N_{ai} \\ (a = 1, \dots, m&; i = 1, \dots, n) \end{align*}\] [If $M, N$ represent linear maps $T, S : V \to W$, then $\alpha M + \beta N$ represents $\alpha T + \beta S$, all w.r.t. same choice of bases].

4.5.2 Matrix multiplication

If $A$ is an $m \times n$ matrix, entries $A_{ai} \in \mathbb{R}$ or $\mathbb{C}$
and $B$ is an $n \times p$ matrix, entries $B_{ir}$ then $AB$ is an $m \times p$ matrix defined by $(AB)_{ar} = A_{ai} B_{ir}$ ($\sum$ convention). The product $AB$ is not defined unless no. of cols of $A =$ no. of rows of B. \[\begin{align*} a &= 1, \dots, m \\ i &= 1, \dots, n \\ r &= 1, \dots, p. \end{align*}\]

Matrix multiplication corresponds to the composition of linear maps. \[\begin{align*} [(AB) \underline{x}]_a &= (AB)_{ar} x_r \text{ and compare} \\ [A(B \underline{x})]_a &= A_{ai}(B \underline{x})_i = A_{ai} (B_{ir} x_r) \\ &= (A_{ai} B_{ir}) x_r \end{align*}\]

Example 4.13 \[\begin{align*} A &= \begin{pmatrix}1 & 3 \\-5 & 0 \\2 & 1\end{pmatrix},\ B = \begin{pmatrix}1 & 0 & -1 \\2 & -1 & 3\end{pmatrix} \\ AB &= \begin{pmatrix} 7 & -3 & 8 \\ -5 & 0 & 5 \\ 4 & -1 & 1 \end{pmatrix} \\ BA &= \begin{pmatrix} -1 & 2 \\ 13 & 9 \end{pmatrix} \end{align*}\]

4.5.2.1 Helpful points of view

Regarding $\underline{x} \in \mathbb{R}^n$ as a col vec or $n \times 1$ matrix, definition on matrix multiplication a matrix or vector agree.
For product of $\underbrace{A}_{m \times n} \underbrace{B}_{n \times p}$ have columns $\underline{C}_r (B) \in \mathbb{R}^n$ and $\underline{C}_r (AB) \in \mathbb{R}^m$ related by $\underline{C}_r (AB) = A \underline{C}_r (B)$
\[\begin{align*} AB &= \begin{pmatrix} & \vdots & \\ \longleftarrow & \underline{R}_a (A) & \longrightarrow \\ & \vdots & \end{pmatrix} \begin{pmatrix} & \big\uparrow & \\ \dots & \underline{C}_r(B) & \dots \\ & \big\downarrow & \end{pmatrix} \\ (AB)_{ar} &= [\underline{R}_a (A)]_i [\underline{C}_r (B)]_i \\ &= \underline{R}_a (A) \cdot \underline{C}_r (B) \text{ dot product in $\mathbb{R}^n$ for real matrices.} \end{align*}\]

4.5.2.2 Properties of matrix products

\[\begin{align*} (\lambda M + \mu N) P &= \lambda (MP) + \mu (NP) \\ P(\lambda M + \mu N) &= \lambda (PM) + \mu (PN) \\ (MN)P &= M (NP) \end{align*}\]

4.5.3 Matrix Inverses

Consider $A$ $m \times n$ matrix and $B, C$ $n \times m$ matrices, $B$ is a left inverse for $A$ if \[\begin{align*} BA = I_n; \end{align*}\] $C$ is a right inverse for $A$ if \[\begin{align*} AC = I_m. \end{align*}\]

If $m = n$, $A$ is square, one of these implies the other and $B = C = A^{-1}$, the inverse. \[\begin{align*} A A^{-1} = A^{-1} A = I. \end{align*}\] Not every matrix has an inverse; if it does it is called invertible or non-singular.

Consider map $\mathbb{R}^n \to \mathbb{R}^n$ given by real matrix $M$. If $\underline{x}' = M \underline{x}$ and $M^{-1}$ exists then $\underline{x} = M^{-1} \underline{x}'$.
For $n = 2$ \[\begin{align*} x_1' &= M_{11} x_1 + M_{12} x_2 \\ x_2' &= M_{21} x_1 + M_{22} x_2 \\ \implies M_{22} x_1' - M_{12} x_2' &= (\det M) x_1 \\ \text{and } - M_{21} x_1' + M_{11} x_2' &= (\det M) x_2 \end{align*}\] So if $\det M = M_{11} M_{22} - M_{12} M_{21} \neq 0$ then $M^{-1} = \frac{1}{\det M} \begin{pmatrix} M_{22} & -M_{12} \\ -M_{21} & M_{11} \end{pmatrix}$.

Example 4.14 \[\begin{align*} R (\theta) &= \begin{pmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \\ R(\theta)^{-1} &= R (-\theta) \end{align*}\]

Example 4.15 Reflection. \[\begin{align*} H (\theta) &= \begin{pmatrix} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{pmatrix} \\ H(\theta)^{-1} &= H (\theta) \end{align*}\]

Example 4.16 \[\begin{align*} S (\lambda) &= \begin{pmatrix} 1 & \lambda \\ 0 & 1 \end{pmatrix} \\ S(\lambda)^{-1} &= S (-\lambda) \end{align*}\]

4.5.4 Transpose and Hermitian Conjugate

4.5.4.1 Transpose

Definition 4.2 (Transpose) If $M$ is an $m \times n$ matrix, the transpose $M^T$ is an $n \times m$ matrix defined by \[\begin{align*} (M^T)_{ia} &= M_{ai} \ ``\text{exchange rows and columns"} \\ [a &= 1, \dots, m;\ i = 1, \dots, n] \end{align*}\]

4.5.4.1.1 Properties

\[\begin{align*} (\alpha A + \beta B)^T &= \alpha A^T + \beta B^T \ (A, B \ m \times n) \\ (AB)^T &= B^T A^T \\ \text{Check: } [(AB)^T]_{ra} &= (AB)_{ar} \\ &= A_{ai} B_{ir} \ \left(\sum \text{ convention} \right) \\ &= (A^T)_{ia} (B^T)_{ri} \\ &= (B^T)_{ri} (A^T)_{ia} \\ &= (B^T A^T)_{ra} \end{align*}\]

Note: $\underline{x} = \begin{pmatrix}x_1 \\\vdots \\x_n\end{pmatrix}$ is a column vector or a $n \times 1$ matrix.
$\implies \underline{x}^T = \begin{pmatrix}x_1 & \dots & x_n\end{pmatrix}$ is a row vector or $1 \times n$ matrix.
Inner product on $\mathbb{R}^n$ is $\underline{x} \cdot \underline{y} = \underline{x}^T \underline{y}$, a scalar or $1 \times 1$ matrix, but $\underline{y} \underline{x}^T = M$, a $n \times n$ matrix with $M_{ij} = y_i x_j$.

Definition 4.3 (Symmetric and Antisymmetric matrix) If $M$ is square, $n \times n$, then $M$ is symmetric iff $M^T = M$ or $M_{ij} = M_{ji}$ and antisymmetric iff $M^T = - M$ or $M_{ij} = - M_{ji}$.

Any square matrix can be written as a sum of a symmetric and antisymmetric parts: \[\begin{align*} M = S + A \text{ where } S &= \frac{1}{2} (M + M^T) \\ \text{and } A &= \frac{1}{2} (M - M^T) \end{align*}\]

Example 4.17 If $A$ is $3 \times 3$ antisymmetric, then it can be rewritten in terms of vec $\underline{a}$ \[\begin{align*} A &= \begin{pmatrix} 0 & a_3 & -a_2 \\ -a_3 & 0 & a_1 \\ a_2 & -a_1 & 0 \end{pmatrix} \\ A_{ij} &= \epsilon_{ijk} a_k \text{ and } a_k = \frac{1}{2} \epsilon_{kij} A_{ij} \\ \text{Then } (A \underline{x})_i &= A_{ij} x_j = \epsilon_{ijk} a_k x_j \\ &= (\underline{x} \wedge \underline{a})_i \end{align*}\]

4.5.4.2 Hermitian Conjugate

Definition 4.4 (Hermitian Conjugate) If $M$ is a $m \times n$ matrix the hermitian conjugate $M^\dagger$ is defined by $(M^\dagger)_{ia} = \overline{M}_{ai}$ or $M^\dagger = \overline{M}^T = \overline{M^T}$

4.5.4.2.1 Properties

\[\begin{align*} (\alpha A + \beta B)^\dagger &= \overline{\alpha} A^\dagger + \overline{\beta} B^\dagger \\ (AB)^\dagger &= B^\dagger A^\dagger \end{align*}\]

Note: $\underline{z} = \begin{pmatrix}x_1 \\\vdots \\x_n\end{pmatrix}$ is a column vector or a $n \times 1$ matrix.
$\implies \underline{z}^\dagger = \begin{pmatrix}x_1 & \dots & x_n\end{pmatrix}$ is a row vector or $1 \times n$ matrix.
Inner product on $\mathbb{C}^n$ is $(\underline{z}, \underline{w}) = \underline{z}^\dagger \underline{w}$, a scalar or $1 \times 1$ matrix.

Definition 4.5 (Hermitian and Anti-Hermitian matrix) If $M$ is square $n \times n$ then $M$ is hermitian if $M^\dagger = M$ or $M_{ij} = \overline{M}_{ji}$ and anti-hermitian if $M^\dagger = - M$ or $M_{ij} = - \overline{M}_{ji}$.

4.5.4.3 Trace

Definition 4.6 (Trace) For any square $n \times n$ matrix $M$, the trace is defined by \[\begin{align*} \operatorname{tr} (M) = M_{ii} \text{ (the sum of diagonal entries.)} \end{align*}\]

4.5.4.3.1 Properties

\[\begin{align*} \operatorname{tr} (\alpha M + \beta N) &= \alpha \operatorname{tr} (M) + \beta \operatorname{tr}(N) \\ \operatorname{tr} (MN) &= \operatorname{tr} (NM) \\ [ \text{check : } (MN)_{ii} &= M_{ia} N_{ai} \\ &= N_{ai} M_{ia} \\ &= (NM)_{aa} ] \\ \operatorname{tr} (M) &= \operatorname{tr} (M^T) \\ \operatorname{tr} (I_n) &= n \\ [I_{ij} = \delta_{ij} \text{ and } I_{ii} = \delta_{ii} = n] \end{align*}\]

We previously decomposed $M = S + A$ (symmetric/ anti-symmetric parts).
Let $T = S - \frac{1}{n} (\operatorname{tr} (S)) I$ or $T_{ij} = S_{ij} - \frac{1}{n} \operatorname{tr} (S) \delta_{ij}$, then $T_{ii} = \operatorname{tr}(T) = 0$; and note $\operatorname{tr}(M) = \operatorname{tr}(S)$ and $\operatorname{tr}(A) = 0$⁷. So $M = \underset{\text{symm and traceless}}{T} + \underset{\text{antisymm part}}{A} + \underset{\text{pure trace}}{\frac{1}{n} \operatorname{tr}(M) I}$

Example 4.18 \[\begin{align*} M &= \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 1 & 2 & 3 \end{pmatrix} \\ S &= \begin{pmatrix} 1 & 3 & 2 \\ 3 & 4 & 5 \\ 2 & 4 & 3 \end{pmatrix} \text{ and } A = \begin{pmatrix} 0 & -1 & 1 \\ 1 & 0 & 2 \\ -1 & -2 & 0 \end{pmatrix} \\ \operatorname{tr}(S) &= \operatorname{tr}(M) = 9 \\ T &= \begin{pmatrix} -2 & 3 & 2 \\ 3 & 2 & 4 \\ 2 & 4 & 0 \end{pmatrix} \\ M &= T + A + 3I \\ \text{Furthermore } A \underline{x} &= \underline{x} \wedge \underline{a} \text{ where } \underline{a} = \begin{pmatrix}2 & -1 & -1\end{pmatrix}. \end{align*}\]

4.6 Orthogonal and Unitary Matrices

Definition 4.7 (Orthogonal matrix) A real $n \times n$ matrix is orthogonal iff \[\begin{align*} u^T u &= u u^T = I \\ \text{i.e. } u^T &= u^{-1}. \end{align*}\]

These conditions can be written \[\begin{align*} (u^T u)_{ij} &= (u u^T)_{ij} = I_{ij} \\ \underbrace{u_{ki} u_{kj}}_\text{cols of $u$ are othornormal} &= \underbrace{u_{ik} u_{jk}}_\text{rows of $u$ are othornormal} = \delta_{ij} \end{align*}\] [recall $[\underline{C}_i (u)]_k = u_{ki} = [R_k(u)]_i$]

\[\begin{align*} \underbrace{\begin{pmatrix} & \vdots & \\ \longleftarrow & \underline{C}_i & \longrightarrow \\ & \vdots & \end{pmatrix}}_{u^T} \underbrace{\begin{pmatrix} & \big\uparrow & \\ \dots & \underline{C}_j & \dots \\ & \big\downarrow & \end{pmatrix}}_{u} &= I \\ \underline{C}_i \cdot \underline{C}_j = \delta_{ij} \end{align*}\]

Equivalent definition: u is orthogonal iff it preserves the inner product on $\mathbb{R}^n$. \[\begin{align*} (u \underline{x}) \cdot (u \underline{y}) &= \underline{x} \cdot \underline{y} \quad \forall \; x, y \in \mathbb{R}^n \end{align*}\] To check equivalence, write this as \[\begin{align*} (u \underline{x}) \cdot (u \underline{y}) &= x^T (u^T u) y \\ &= x^T y \iff u^T u = I \\ &= \underline{x} \cdot \underline{y} \quad \forall \; x, y \in \mathbb{R}^n \end{align*}\] Note, since $\underline{C}_i = u \underline{e}_i$, columns being orthonormal $\iff (u \underline{e}_i) \cdot (u \underline{e}_j) = \underline{e}_i \cdot \underline{e}_j = \delta_{ij}$.

Example 4.19 In $\mathbb{R}^2$ we found all orthogonal matrices Isometries, area and determinants in $\mathbb{R}^2$:
rotations $R(\theta) = \begin{pmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}$ and reflections $H(\theta) = \begin{pmatrix} \cos \theta & \sin \theta \\\sin \theta & - \cos \theta \end{pmatrix}$. Clearly $R(\theta)^T = R(-\theta) = R(\theta)^{-1}$. \[\begin{align*} R(\theta)^T &= R(-\theta) = R(\theta)^{-1} \\ H(\theta)^T &= H(\theta) = H(\theta)^{-1}. \end{align*}\] In $\mathbb{R}^3$ we found the matrix $R(\theta)$ for rotation through $\theta$ about axis $\underline{n}$, 4.12. \[\begin{align*} R(\theta)^T &= R(-\theta) \\ \text{Since } R(\theta)_{ij} &= R(-\theta)_{ji} \end{align*}\] and can check explicitly \[\begin{align*} R(\theta)^T R(\theta) &= R(-\theta)R(\theta) = I \\ \text{or } R(\theta)_{ki} R(\theta)_{kj} &= \delta_{ij} \end{align*}\]

Definition 4.8 (Unitary matrix) A complex $n \times n$ matrix $u$ is unitary iff \[\begin{align*} u^\dagger u &= u u^\dagger = I \\ \text{i.e. } u^\dagger &= u^{-1}. \end{align*}\]

Equivalent definition: u is unitary iff it preserves the inner product on $\mathbb{C}^n$. \[\begin{align*} (u \underline{z}, u \underline{w}) &= (\underline{z}, \underline{w}) \quad \forall \; z, w \in \mathbb{C}^n \end{align*}\]

To check equivalence, write this as \[\begin{align*} (u \underline{z})^\dagger (u \underline{w}) &= \underline{z}^\dagger (u^\dagger u) \underline{w} \\ &= \underline{z}^\dagger \underline{w} \iff u^\dagger u = I \\ &= (\underline{z}, \underline{w}) \quad \forall \; \underline{z}, \underline{w} \end{align*}\] Note, since $\underline{C}_i = u \underline{e}_i$, columns being orthonormal $\iff (u \underline{e}_i) \cdot (u \underline{e}_j) = \underline{e}_i \cdot \underline{e}_j = \delta_{ij}$.

Mostly concerned with $V = \mathbb{R}^n,\ W = \mathbb{R}^m$ or $V = \mathbb{C}^n,\ W = \mathbb{C}^m$↩︎
$A$ has zeros on its diagonal.↩︎

Vectors and Matrices 2021 - 2022