4 Sets, Functions and Relations

A set is a collection of mathematical objects.
E.g. \(\mathbb{R}, \mathbb{N}, \{1, 5, 9\}, [-2, 3]\).
The order of the elements in the set is immaterial, and elements are counted only once (unlike sequences).
E.g. \(\{1, 3, 7\} = \{1, 7, 3\}\) and \(\{3, 4, 4, 8\} = \{3, 4, 8\}\).

We write \(x \in A\) if \(x\) is an element of the set \(A\), and \(x \notin A\) if not.
Two sets are equal if they have the same elements. That is, if \(\forall \; x, x \in A \iff x \in B\), then \(A = B\). In particular, there is only one empty set \(\emptyset\).

A set \(B\) is a subset of \(A\), written “\(B \subseteq A\)” or “\(B \subset A\)”, if every element of \(B\) is an element of \(A\). 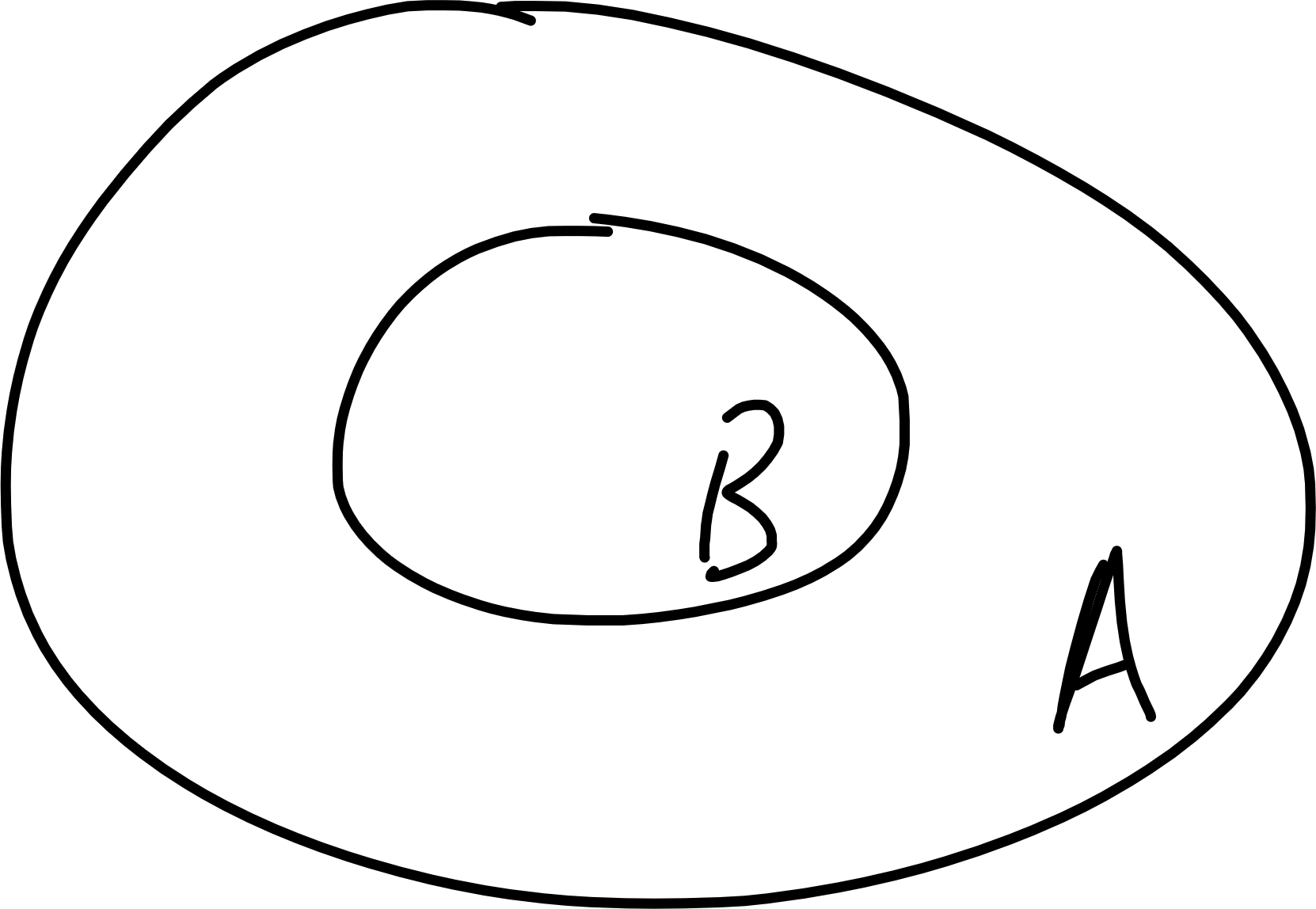\(B\) is said to be a proper subset of \(A\) if \(B \subseteq A\) and \(B \neq A\) (also write \(B \subsetneq A\)).

Note that \(A = B\) iff \(A \subseteq B\) and \(B \subseteq A\).

If \(A\) is a set and \(P\) is a property of (some) elements of \(A\), we can write \(\{x \in A : P(x)\}\) for the subset of \(A\) comprising of those elements for which \(P(x)\) holds, this is called subset selection. E.g. \(\{n \in \mathbb{N} : n \text{ is prime}\} = \{2, 3, 5, 7, 11, \dots\} \subseteq \mathbb{N}\).

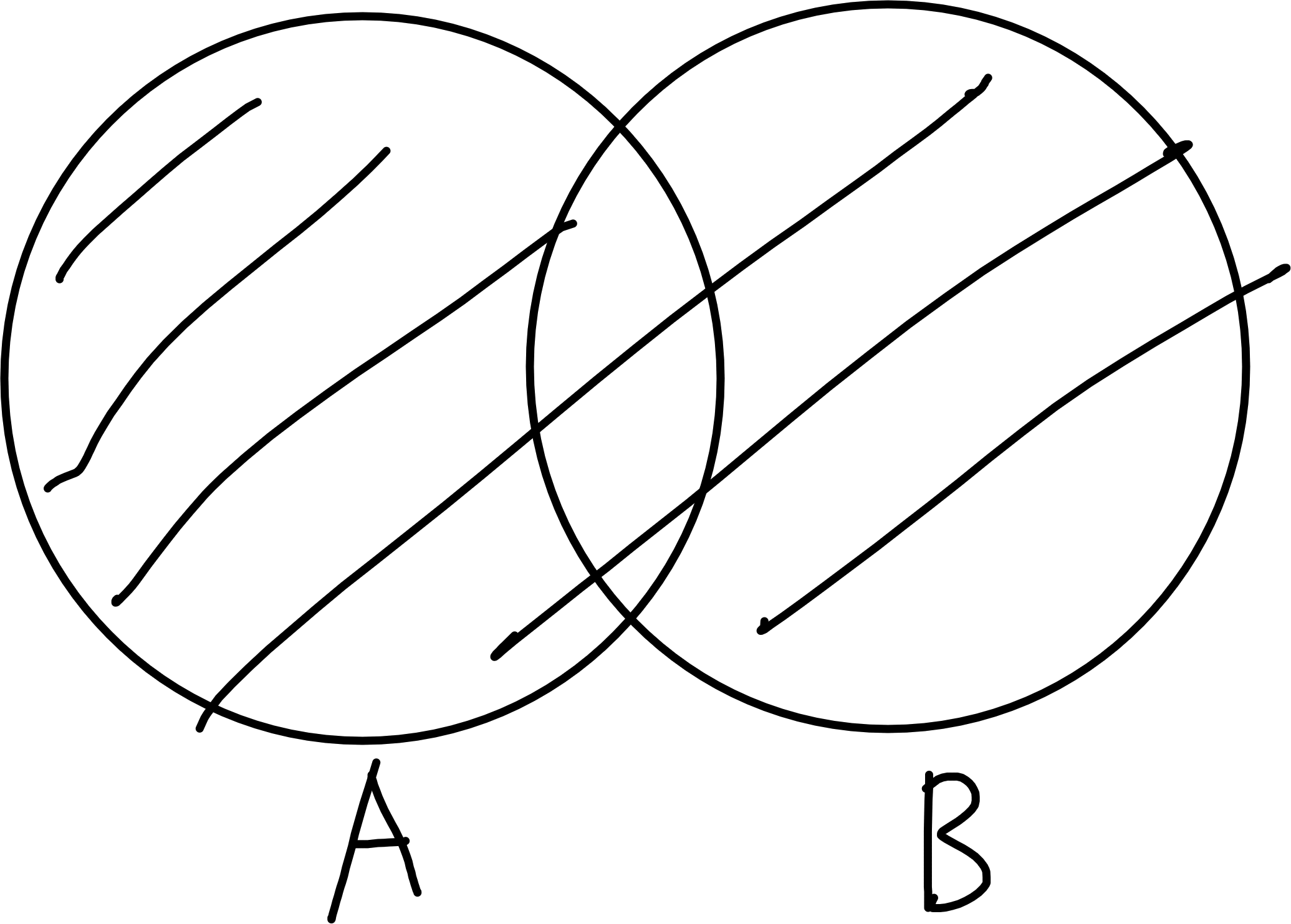
If \(A\) and \(B\) are sets, then their union \(A \cup B\) is \[\begin{align*} A \cup B = \{x : x \in A \text{ or } x \in B\}. \end{align*}\]

Their intersection \(A \cap B\) is defined to be \[\begin{align*} A \cap B = \{x: x \in A \text{ and } x \in B\}. \end{align*}\]

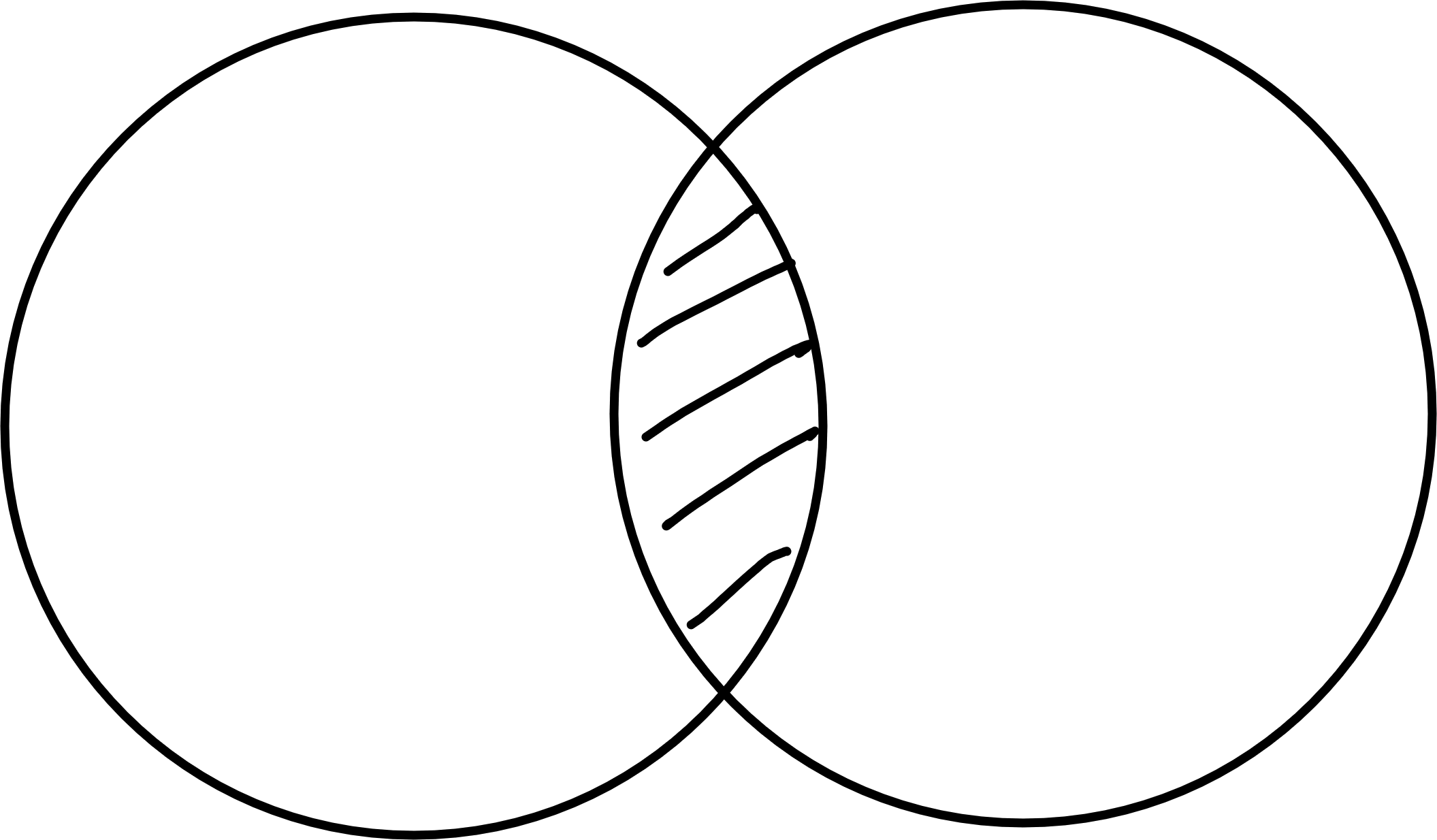
We say \(A\) and \(B\) are disjoint if \(A \cap B = \emptyset\)15 Note that we can view intersection as a special case of subset selection: \(A \cap B = \{x \in A : x \in B\}\).

Similarly, we have the set difference \(A \setminus B = \{x \in A : x \notin B\}\).

Note that \(\cup\) and \(\cap\) are both commutative and associative. Also, \(\cup\) is distributive over \(\cap\), i.e. \[\begin{align*} A \cup (B \cap C) = (A \cup B) \cap (A \cup C), \end{align*}\] and \(\cap\) is distributive over \(\cup\), i.e. \[\begin{align*} A \cap (B \cup C) = (A \cap B) \cup (A \cap C). \end{align*}\]

Proof. To prove \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\), show that LHS \(\subseteq\) RHS and RHS \(\subseteq\) LHS, so LHS \(=\) RHS.

If \(x \in A \cap (B \cup C)\), then \(x \in A\) and \(x \in B \cup C\), so \(x \in A\) and (\(x \in B\) or \(x \in C\)).
If \(x \in B\), then \(x \in A \cap B\), and if \(x \in C\), then \(x \in A \cap C\). Hence, in any case \(x \in (A \cap B) \cup (A \cap C)\).

Conversely, suppose \(x \in (A \cap B) \cup (A \cap C)\), then \(x \in A \cap B\) or \(x \in A \cap C\).
If \(x \in A \cap B\), then \(x \in A\) and \(x \in B \cup C\).
If \(x \in A \cap C\), then \(x \in A\) and \(x \in B \cup C\), so in any case \(x \in A \cap (B \cup C)\).

If \(A_1, A_2, A_3, \dots\) are sets, then \[\begin{align*} \bigcap_{n = 1}^\infty A_n &= A_1 \cap A_2 \cap A_3 \cap \dots \\ &= \{x : x \in A_n \text{ for all } n \in \mathbb{N}\}. \\ \text{Similarly } \bigcup_{n = 1}^\infty A_n &= A_1 \cup A_2 \cup A_3 \cup \dots \\ &= \{x : x \in A_n \text{ for some } n \in \mathbb{N}\}. \end{align*}\] Warning: \(\bigcup_{n = 1}^\infty A_n\) is not the “limit” of anything!

More generally, given an index set \(I\) and a collection of sets \(A_i\) indexed by \(I\) (we have a \(A_i\) for every \(i \in I\)), we write \[\begin{align*} \bigcap_{i \in I} A_i &= \{x : x \in A_i \; \forall \; i \in I\} \\ \text{and } \bigcup_{i \in I} A_i &= \{x : x \in A_i \text{ for some } i \in I\}. \end{align*}\]

Given sets \(A\) and \(B\), we can form their Cartesian product \(A \times B = \{(a, b) : a \in A, b \in B\}\) (“\(A\) cross \(B\)”), which is the set of ordered pairs \((a, b)\) with \(a \in A, b \in B\).
Here \((a, b) = (a', b') \iff a = a' \text{ and } b = b'\).16 We can extend this to ordered triples and so on, e.g. \(\mathbb{R}^3 = \mathbb{R} \times \mathbb{R} \times \mathbb{R}\) \[\begin{align*} \mathbb{R}^3 &= \mathbb{R} \times \mathbb{R} \times \mathbb{R} \\ &= \{(x, y, z) : x \in \mathbb{R}, y \in \mathbb{R}, z \in \mathbb{R}\}. \end{align*}\]

Definition 4.1 (Power set) For any set \(X\), we can form the power set \(\mathcal{P}(X)\) consisting of all subsets of \(X\), that is, \[\begin{align*} \mathcal{P}(X) = \{Y : Y \subseteq X\}. \end{align*}\]

E.g. if \(X = \{1, 2\}\), then \(\mathcal{P}(X) = \left\{\emptyset, \{1\}, \{2\}, \{1, 2\} \right\}\).

Warning: Given a set \(A\), we can form \(\{x \in A: P(x)\}\) for any property \(P\). But we cannot form \(\{x : P(x)\}\). Indeed, suppose \(X = \{x : x \text{ is a set and } x \notin x\}\) were a set.
Then \(X \in X\) implies that \(X \notin X\) ⨳
while \(X \notin X\) implies that \(X \in X\) ⨳.
This is known as Russell’s Paradox.

Similarly, there is no “universal” set \(Y\), meaning that \(\forall \; x \quad x \in Y\). Otherwise we could form \(X\) above by subset selection: \[\begin{align*} X = \{ x \in Y: x \notin x\}. \end{align*}\]

Moral: To guarantee that a given set exists, it should be obtained from known sets (e.g. \(\mathbb{N}, \mathbb{R}\)) in one of the ways described above.

4.1 Finite Sets

Write \(\mathbb{N}_0 = \mathbb{N} \cup \{0\}\), i.e. \(\{0, 1, 2, 3, \dots\}\)17.
Given \(n \in \mathbb{N}_0\), we say a set \(A\) has size \(n\) if we can write \(A = \{a_1, a_2, \dots, a_n\}\) with the elements \(a_i\) distinct. E.g. \(\{1, 3, 7\}\) has size \(3\), \(\emptyset\) has size \(0\).

We say \(A\) is finite if \(\exists \; n \in \mathbb{N}_0\) s.t. \(A\) has size \(n\), and \(A\) is infinite otherwise.

Proposition 4.1 A set of size \(n\) has exactly \(2^n\) subsets.

Proof (1). We may assume that our set is \(\{1, 2, \dots, n\}\).
To specify a subset \(S\) of \(\{1, 2, \dots, n\}\), we must say if \(1 \in S\) or \(1 \notin S\), then if \(2 \in S\) or \(2 \notin S\), and so on.
Hence the number of choices for \(S\) is \[\begin{align*} \underbrace{2}_{1 \in S?} \cdot \underbrace{2}_{2 \in S?} \dots \cdot \underbrace{2}_{n \in S?}= 2^n \end{align*}\]

Proof (2). By induction on \(n\). Clearly true for \(n = 0\). Given \(n > 0\), and \(T \subseteq \{1, 2, \dots, n - 1\}\), how many sets \(S \subseteq \{1, 2, \dots, n\}\) are there s.t. \(S \cap \{1, \dots, n - 1\} = T?\).

There are exactly \(2\), namely \(T\) and \(T \cup \{n\}\).
Hence \[\begin{align*} \text{no. of subsets of } \{1, 2, \dots, n\} &= 2 \times \text{ no. of subsets of } \{1, 2, \dots, n - 1\} \\ &= 2 \cdot 2^{n - 1} \\ &= 2^n. \end{align*}\]

If \(A\) has size \(n\), we write “\(|A| = n\)” or “\(\# A = n\)”.

So Proposition 4.1 says that \(|A| = n \implies |\mathcal{P}(A)| = 2^n\).

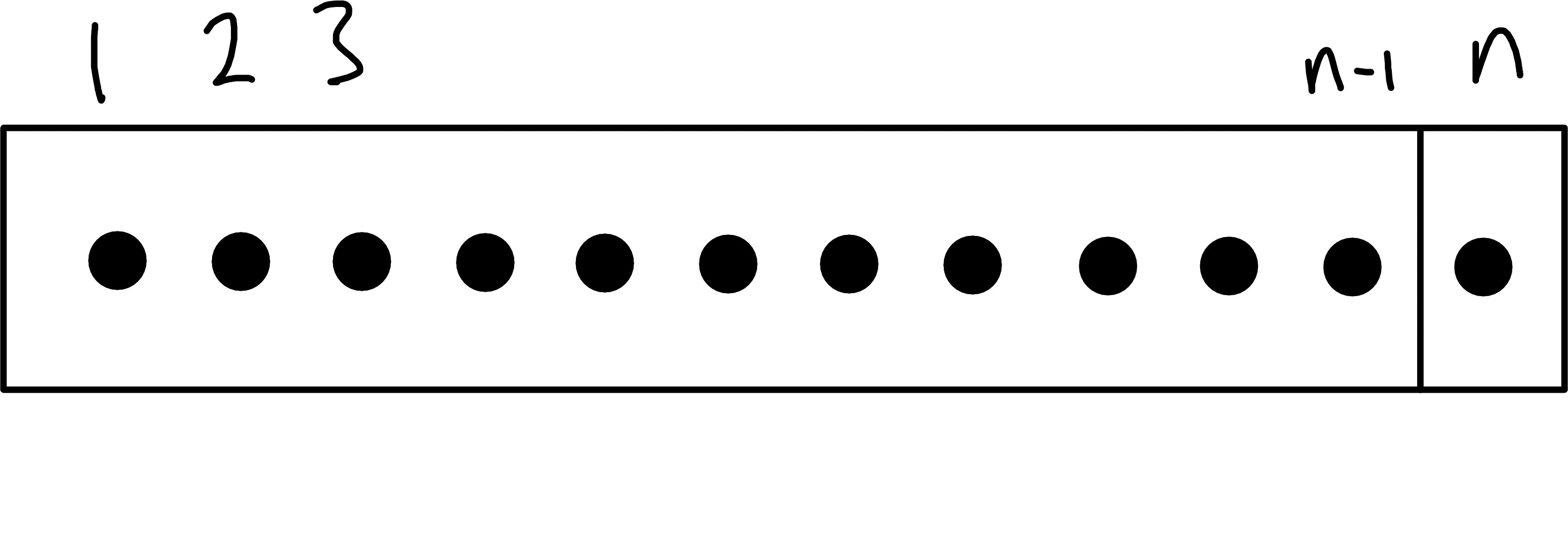
Given \(n \in \mathbb{N}_0\) and \(0 \leq k \leq n\), we write \(\binom{n}{k}\) for the number of subsets of an \(n\)-element set that are of size \(k\). In other words \[\begin{align*} \binom{n}{k} = \left| \{ S \subseteq \{1, 2, \dots, n\} : |S| = k \} \right|. \end{align*}\] \(\binom{n}{k}\) is called a binomial coefficient.

E.g. the subsets of size \(2\) of \(\{1, 2, 3, 4\}\) are precisely \(\{1, 2\}, \{1, 3\}, \{1, 4\}, \{2, 3\}, \{2, 4\}, \{3, 4\}\) so \(\binom{4}{2} = 6\).

Note that by definition \(\binom{n}{0} = 1, \binom{n}{n} = 1, \binom{n}{1} = n\) (\(n > 0\)) and \(\binom{n}{0} + \binom{n}{1} + \binom{n}{2} + \dots + \binom{n}{n-1} + \binom{n}{n} = 2^n\) (the sum of the number of subsets for each size possible). Also, we have \(\binom{n}{k} = \binom{n}{n - k} \ \forall \; n \in \mathbb{N}_0, 0 \leq k \leq n\). E.g. \(\binom{8}{3} = \binom{8}{5}\) Indeed, specifying which \(k\) elements to pick is the same as specifying which \(n - k\) elements not to pick.

Moreover, \(\binom{n}{k} = \binom{n - 1}{k - 1} + \binom{n - 1}{k} \ \forall \; n \in \mathbb{N}, 1 \leq k \leq n - 1\). E.g. \(\binom{8}{3} = \binom{7}{2} + \binom{7}{3}\). Indeed, the number of subsets of \(\{1, 2, \dots, n\}\) of size \(k\) that do not include \(n\) is \(\binom{n - 1}{k}\), while the number of subsets that do include \(n\) is \(\binom{n - 1}{k - 1}\). We obtain Pascal’s triangle. 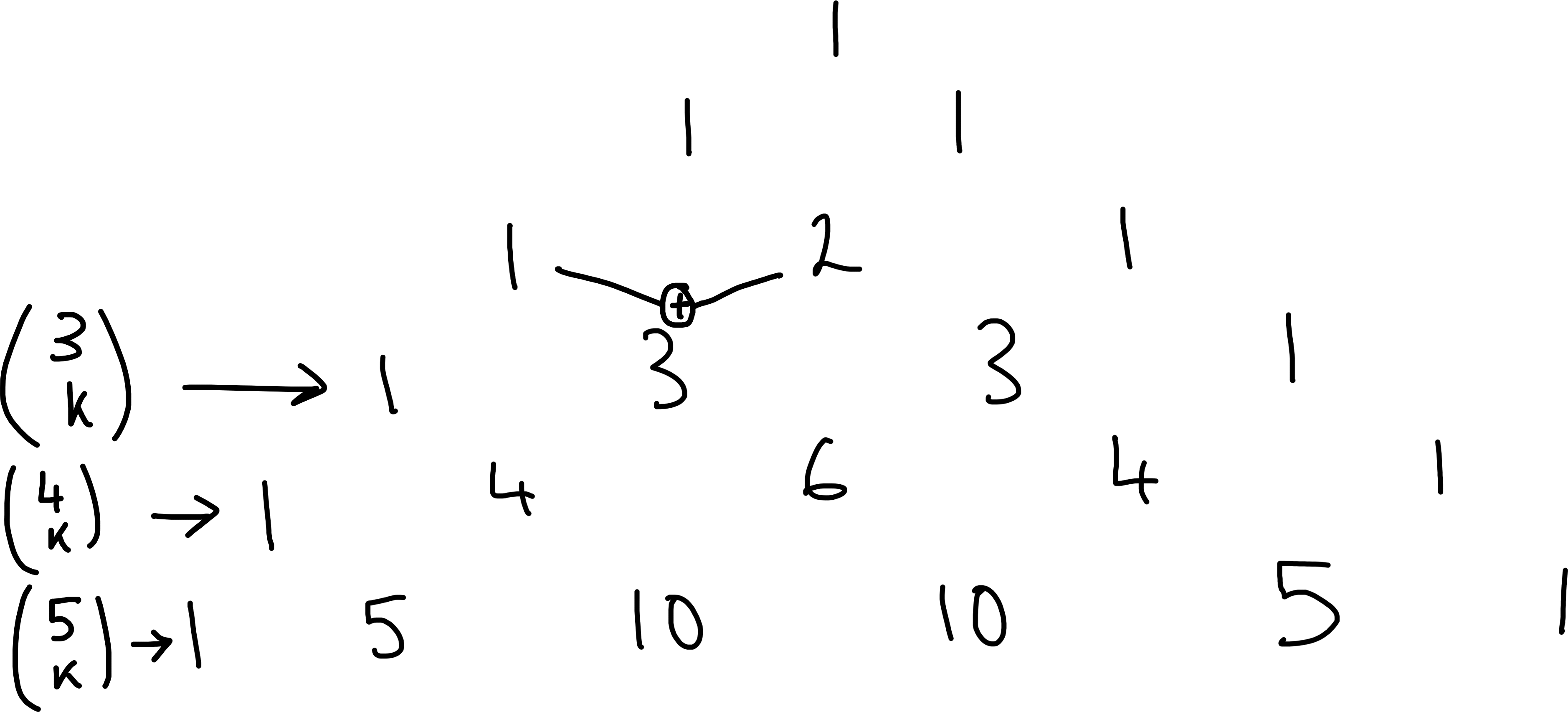Each row starts and ends with a \(1\), and the remaining entities are the sum of the two terms immediately above.

Proposition 4.2 \[\begin{align*} \binom{n}{k} &= \frac{n (n - 1) (n - 2) \dots (n - k + 1)}{k (k - 1) (k - 2) \dots 2 \cdot 1} \\ &= \frac{n!}{k! (n - k)!} \end{align*}\]

Proof. Given a set of size \(n\), there are \(n (n - 1) (n - 2) \dots (n - k + 1)\) ways to pick \(k\) elements, one by one, with unique orders. Each subset of size \(k\) is picked in \(k (k - 1) (k - 2) \dots 2 \cdot 1\) ways by this method. Hence the no. of subsets of size \(k\) in \(\{1, 2, \dots, n\}\) is \(\binom{n}{k} = \frac{n (n - 1) (n - 2) \dots (n - k + 1)}{k (k - 1) (k - 2) \dots 2 \cdot 1}\).

Note that the formula tells us, for example, that \[\begin{align*} \binom{n}{2} &= \frac{n (n - 1)}{2} \sim \frac{n^2}{2} \\ \binom{n}{3} &= \frac{n (n - 1) (n - 2)}{6} \sim \frac{n^3}{6} \text{ for large } n. \end{align*}\]

Theorem 4.1 (Binomial Theorem) For all \(a, b \in \mathbb{R}, n \in \mathbb{N}\) \[\begin{align*} (a + b)^n &= \binom{n}{0} a^n + \binom{n}{1} a^{n - 1} b + \binom{n}{2} a^{n - 2} b^2 + \dots + \binom{n}{n - 1} a b^{n-1} + \binom{n}{n} b^n. \end{align*}\]

Proof. When we expand \((a + b)^n = (a + b) (a + b) \dots (a + b)\) we obtain terms of the form \(a^{n - k} b^k\) \(0 \leq k \leq n\), and the number of terms of the form \(a^{n -k} b^k\) is \(\binom{n}{k}\) as we must specify \(k\) brackets from which to pick \(b\). \[\begin{align*} \text{Hence } (a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k \end{align*}\]

Example 4.1 \((1 + x)^n = 1 + nx + \frac{n (n - 1)}{2} x^2 + \binom{n}{3} x^3 + \dots + \binom{n}{n - 1} + x^n\) so for small \(x\), a good approximation is \(1 + nx\). E.g. \((1.00001)^8 \sim 1.00008\).
A better approximation is \(1 + nx + \frac{n(n-1)}{2}x^2\), e.g. \((1.00001)^8 \sim 1.00008 + 28 (0.00001)^2\).

What can we say about the relationship between sizes of unions and intersections of finite sets?

For example \(|A \cup B| = |A| + |B| - |A \cap B|\) (otherwise elements in the intersection are counted twice.)

Also \(|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |A \cap C| + |A \cap B \cap C|\).

Theorem 4.2 (Inclusion-Exclusion Principle) Let \(S_1, S_2, \dots, S_n\) be finite sets. Then \[\begin{align*} |S_1 \cup S_2 \cup \dots \cup S_n| &= \sum_{|A|=1} |S_A| - \sum_{|A| = 2 } |S_A| + \sum_{|A| = 3 } |S_A| + \dots + (-1)^{n + 1} \sum_{|A| = n } |S_A| \\ \text{where } S_A &= \bigcap_{i \in A} S_i \\ \text{ and } \sum_{|A| = k } |S_A| &\text{ is taken over all } A \subseteq \{1, 2, \dots, n\} \text{ of size } k. \\ \text{Equivalently } \left | \bigcup_{i = 1}^n S_i \right| &= \sum_{k=1}^{n} (-1)^{k + 1} \sum_{A \subseteq \{1, 2, \dots, n\}, |A| = k} \left | \bigcap_{i \in A} S_i \right |. \end{align*}\]

Proof. Let \(x \in S_1 \cup S_2 \cup \dots \cup S_n\), suppose \(x \in S_i\) for \(k\) of the \(S_i\). We want \(x\) to be counted exactly once in the RHS.
Indeed, \(\# \{A : |A| = 1 \text{ with } x \in S_A\} = k\) (gets counted \(k\) times in the first term of the sum) and \(\# \{A : |A| = 2 \text{ with } x \in S_A\} = \binom{k}{2}\). In general, \(\# \{A : |A| = r \text{ with } x \in S_A\} = \binom{k}{r}\) for \(r \leq k\) and \(0\) for \(r > k\).
Thus the number of times \(x\) is counted on the RHS is \[\begin{align*} k - \binom{k}{2} + \binom{k}{3} - \dots + (-1)^{k + 1} \binom{k}{k} &= 1 - \underbrace{\left( 1 - k + \binom{k}{2} - \binom{k}{3} + \dots - (-1)^{k + 1} \binom{k}{k} \right)}_{= (1 + (-1))^k \text{ by the Binomial Theorem}} \\ &= 1 \text{ for } k \geq 1. \end{align*}\]

4.2 Functions

Definition 4.2 (Function) Given sets \(A\) and \(B\), a function \(f\) from \(A\) to \(B\) is a “rule” that assigns to every \(x \in A\) a unique element \(f(x) \in B\).

More formally, a function from \(A\) to \(B\) is a subset \(f \subseteq A \times B\) s.t. for all \(x \in A\), there is a unique \(y \in B\) s.t. \((x, y) \in f\).
If \(f\) is a function from \(A\) to \(B\), we write \(f : A \to B\). If \((x, y) \in f\), we can write \(f(x) = y\), or \(x \mapsto y\)18.

Example 4.2

  1. \[\begin{align*} f : \mathbb{R} &\to \mathbb{R} \text{ is a function} \\ x &\mapsto x^2. \end{align*}\]

  2. \[\begin{align*} f : \mathbb{R} &\to \mathbb{R} \text{ is } \textit{not} \text{ a function, } f(0) = ? \\ x &\mapsto \frac{1}{x} \end{align*}\]

  3. \[\begin{align*} f : \mathbb{R} &\to \mathbb{R} \text{ is } \textit{not} \text{ a function, } \\ x &\mapsto \pm \sqrt{x}. \end{align*}\]

  4. \[\begin{align*} f : \mathbb{R} &\to \mathbb{R} \text{ is a function} \\ x &\mapsto \begin{cases} 1 & \text{if } x \text{ is rational} \\ 0 & \text{otherwise}. \end{cases} \end{align*}\]

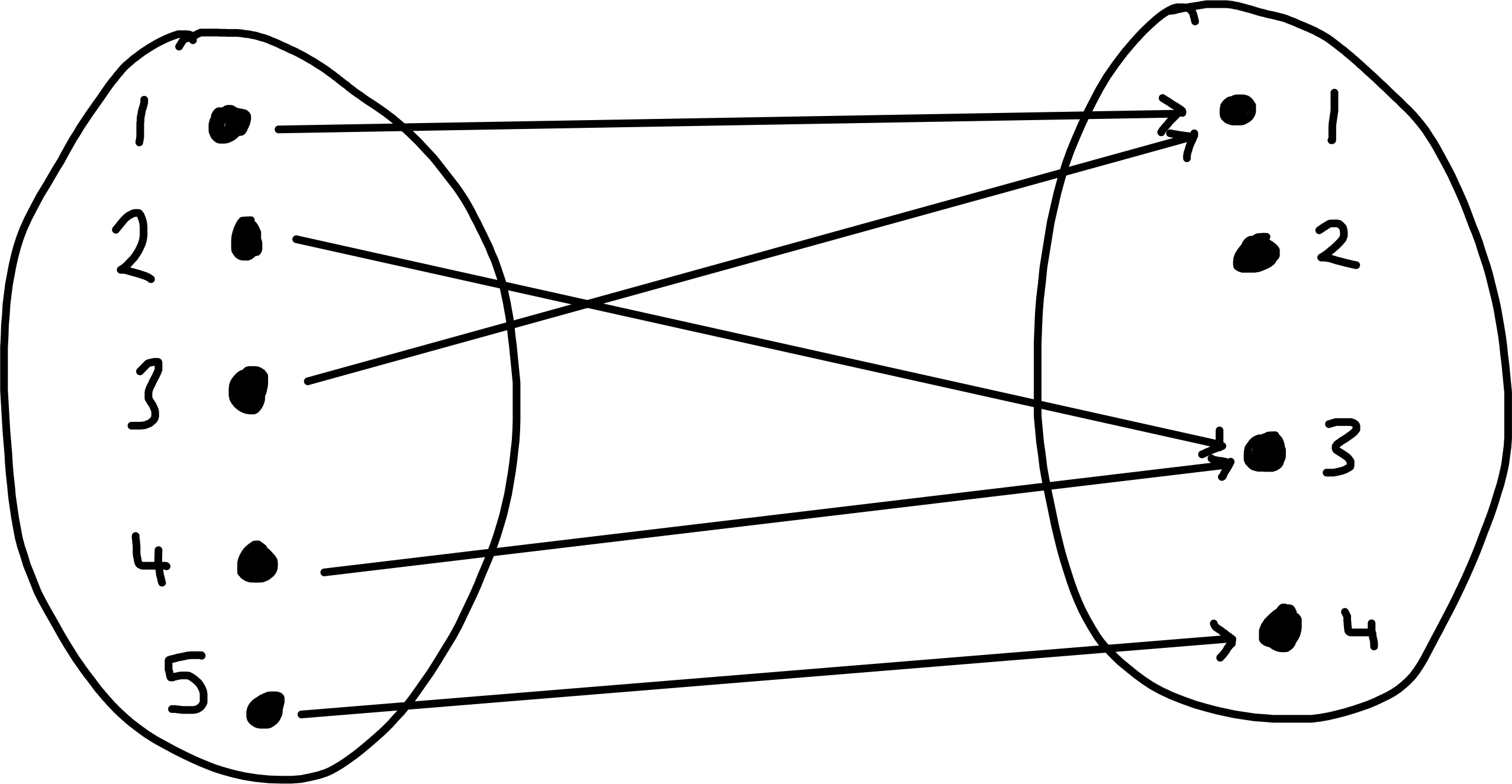
  5. \(f : \{1, 2, 3, 4, 5\} \to \{1, 2, 3, 4\}\) is given by

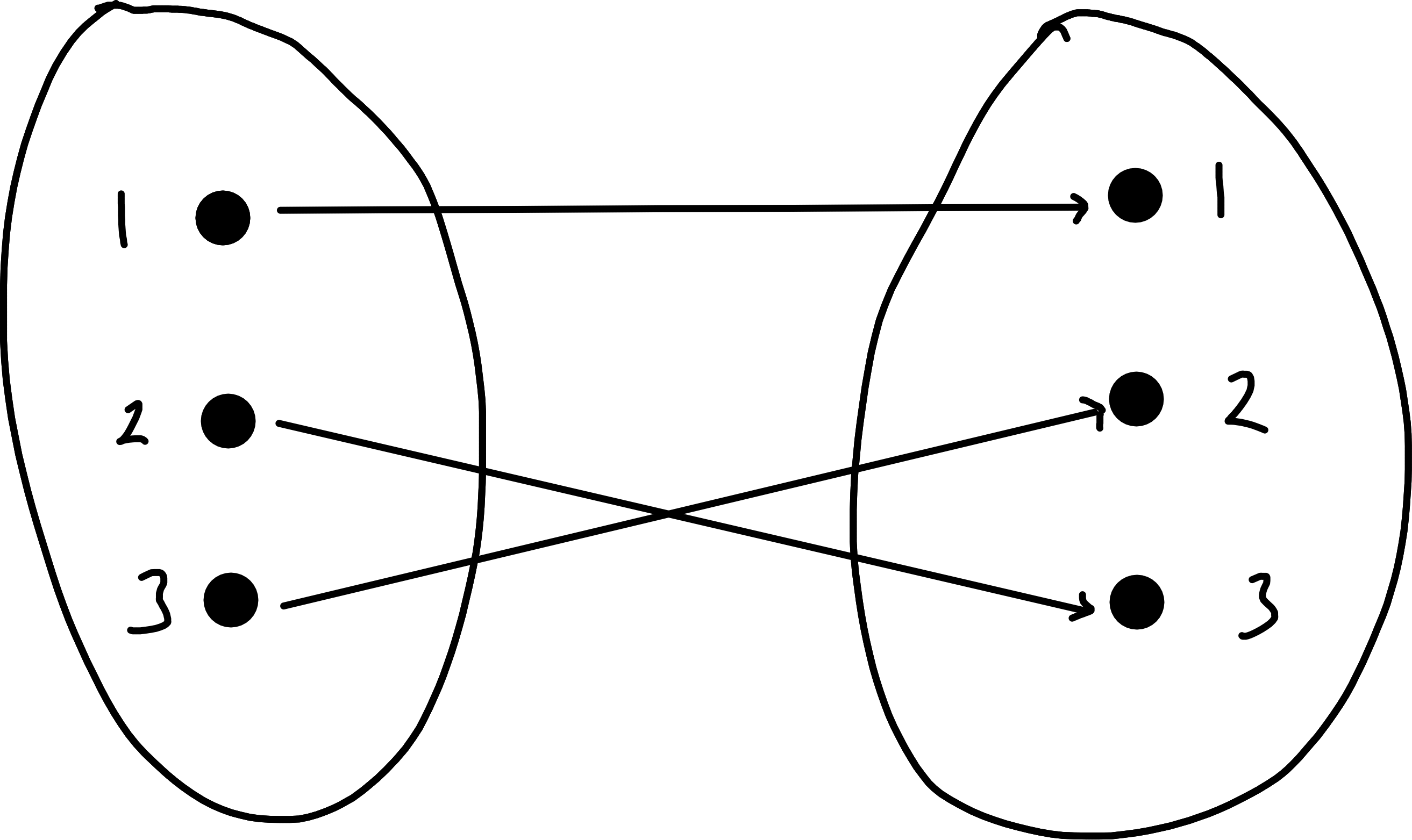
  6. \(f: \{1, 2, 3\} \to \{1, 2, 3\}\)

  7. \(f: \{1, 2, 3\} \to \{1, 2, 3, 4\}\)

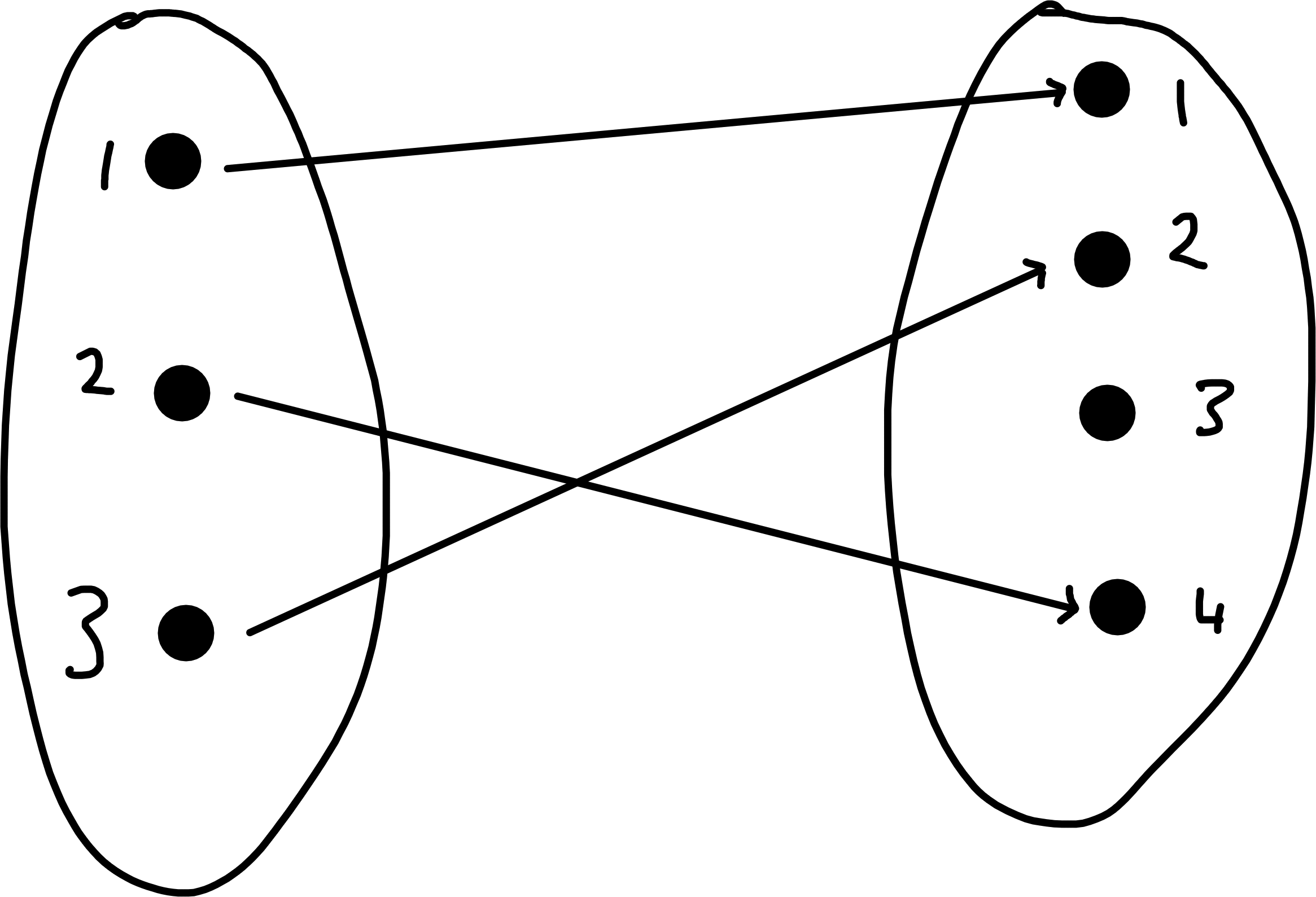
  8. \(f : \{1, 2, 3, 4\} \to \{1, 2, 3\}\)

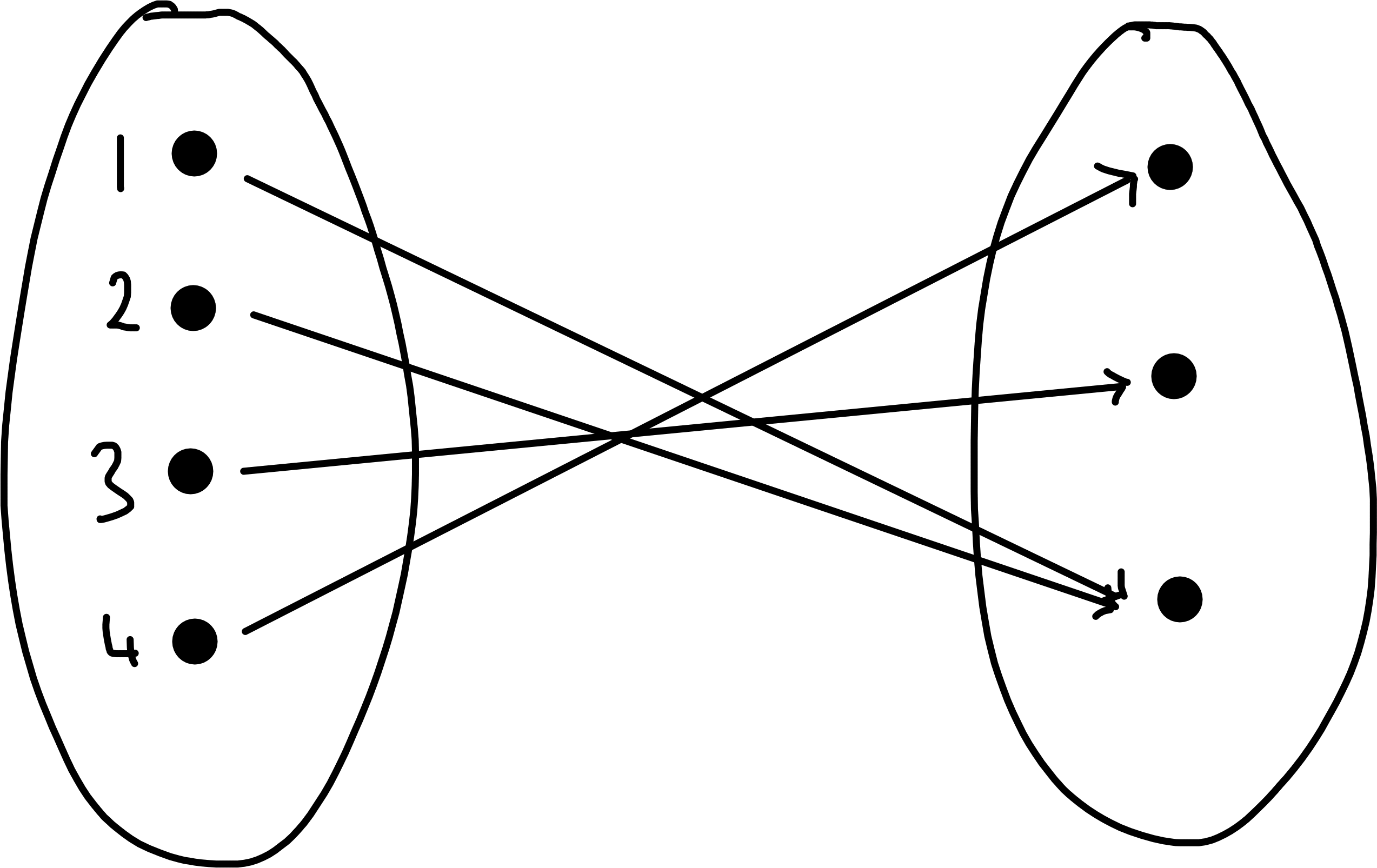
5 - 8 are all functions

Definition 4.3 (Injective function) We say \(f : A \to B\) is injective if \(\forall \; a, a' \in A, a \neq a' \implies f(a) \neq f(a')\).
Equivalently, \(f\) is injective if \(f(a) = f(a') \implies a = a'\).

Examples 6, 7 are injective whilst 5, 8 are not.

Definition 4.4 (Surjective function) We say \(f : A \to B\) is surjective if \(\forall \; b \in B, \exists \; a \in A\) s.t. \(f(a) = b\).

Examples 6, 8 are surjective whilst 5, 7 are not.

Definition 4.5 (Bijective function) We say \(f : A \to B\) is bijective if it is both injective and surjective.

If \(f : A \to B\) is a bijection, then everything in \(B\) is hit (surjective) exactly once (injective) (that is \(f\) pairs the elements of \(A\) and \(B\)).

Example 6 is the only bijection.

Definition 4.6 (Permutation) A permutation of a set \(A\) is a bijection from \(A \to A\).

Given \(f : A \to B\), we say \(A\) is the domain of \(f\) and \(B\) is its range. The image of \(f\), sometime denoted \(\operatorname{im}(f)\), is the set \[\begin{align*} f(A) &= \{f(a) : a \in A \} \\ &= \{b \in B : f(a) = b \text{ for some } a \in A\}. \end{align*}\]

Example 4.3 If \[\begin{align*} f : \mathbb{R} &\to \mathbb{R} \\ x &\mapsto x^2 \\ \operatorname{im}(f) &= \{y \in \mathbb{R} : y \geq 0\}. \end{align*}\]

When specifying a function we must specify its domain and range. E.g. “Is the function \(f(x) = x^2\) injective?” is meaningless, as \(f : \mathbb{N} \to \mathbb{N}\) is injective but \(f : \mathbb{Z} \to \mathbb{Z}\) is not.

4.2.1 Observations

  1. \(f\) is surjective iff \(f(A) = B\). In particular, if \(|B| > |A|\), then there can be no surjection from \(A\) to \(B\).

  2. There can be no injection from \(A\) to \(B\) if \(|A| > |B|\).

  3. If \(f: A \to A\), then \(f\) is injective \(\iff\) \(f\) is surjective.

  4. There is no bijection from \(A\) to any proper subset of \(A\).

Note that (3) and (4) do not hold for infinite sets:
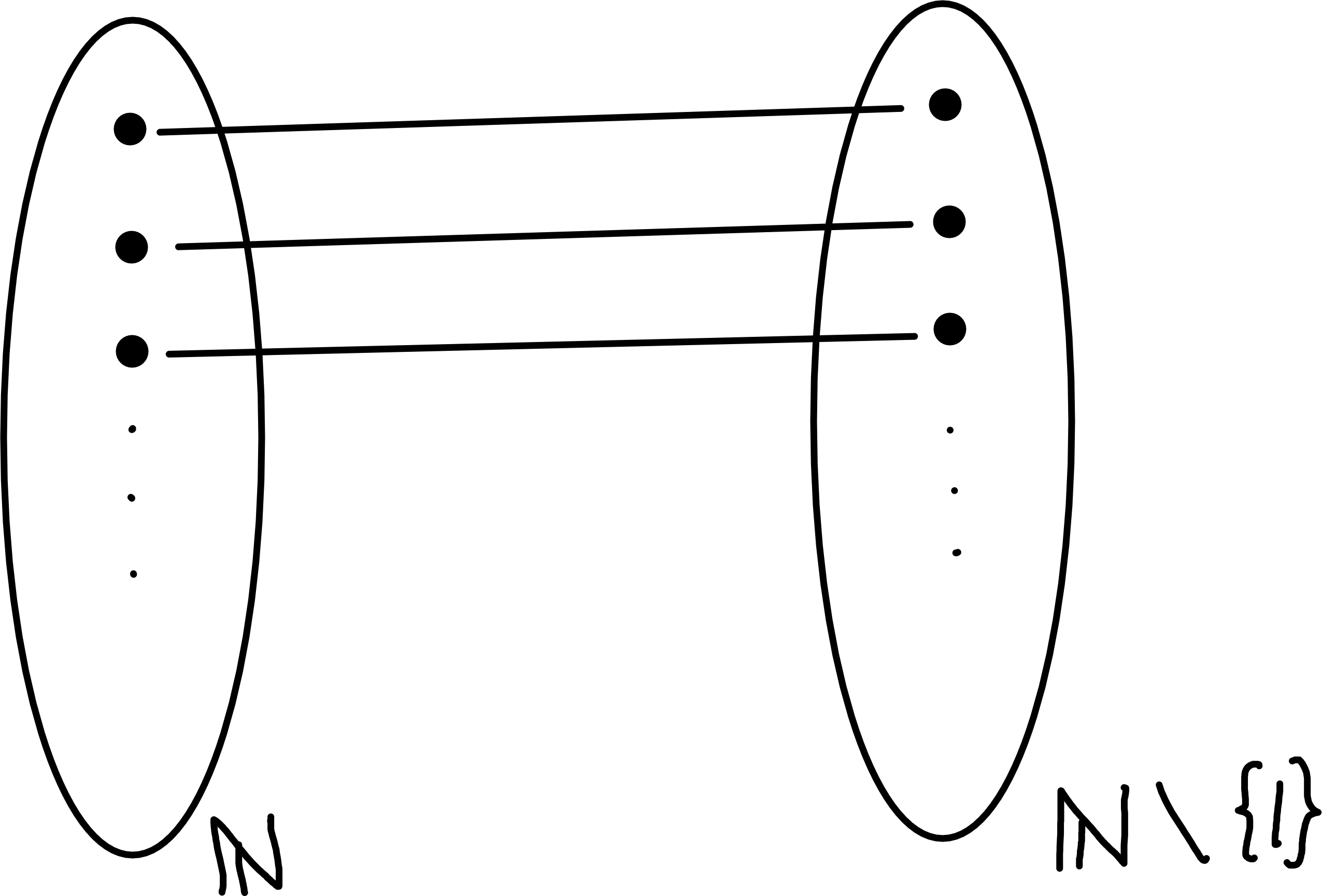
a) \[\begin{align*} f: \mathbb{N} &\to \mathbb{N} \\ x &\mapsto x + 1 \end{align*}\] is injective but not surjective.

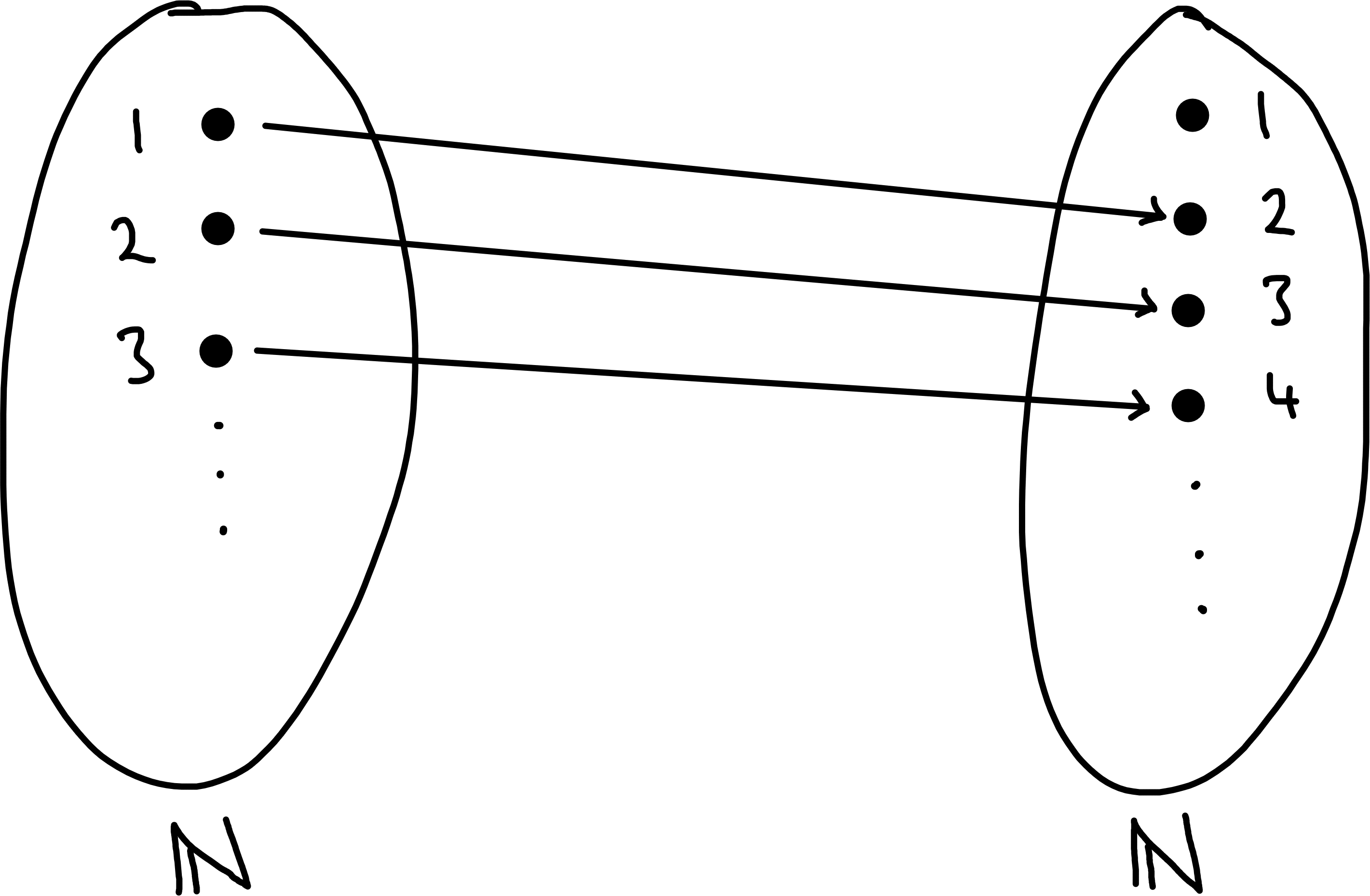
  1. \[\begin{align*} g : \mathbb{N} &\to \mathbb{N} \\ x &\mapsto \begin{cases} x - 1 & \text{if } x \neq 1 \\ 1 & \text{if } x = 1 \end{cases} \end{align*}\] is surjective but not injective

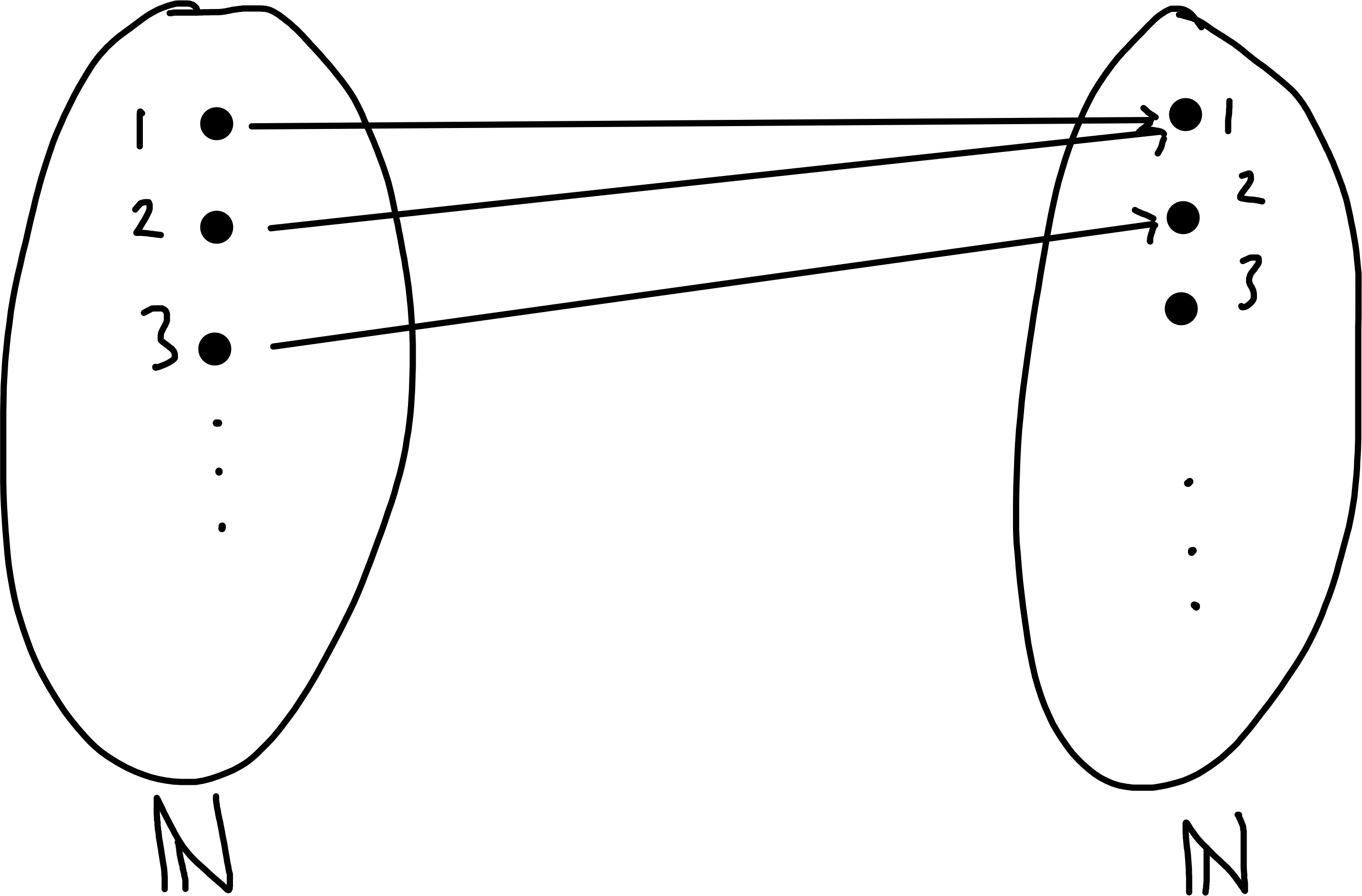
  2. \[\begin{align*} h : \mathbb{N} &\to \mathbb{N} \setminus \{1\} \\ x &\mapsto x + 1 \end{align*}\] is a bijection from \(\mathbb{N}\) to a proper subset of \(\mathbb{N}\).

Example 4.4 (Further examples)

  1. For any set \(X\), we have the identity function \[\begin{align*} \text{id}_X : X &\to X \\ x &\mapsto x. \end{align*}\]

  2. Given a set \(X\) and \(A \subseteq X\), we have the indicator function (or characteristic function) of \(A\) \[\begin{align*} 1_A : X &\to \{0, 1\} \\ x &\mapsto \begin{cases} 1 & \text{if } x \in A \\ 0 & \text{if } x \notin A. \end{cases} \end{align*}\]

  3. A sequence of reals \(x_1, x_2, \dots\) is a function from the natural numbers to the reals \[\begin{align*} \mathbb{N} &\to \mathbb{R} \\ n &\mapsto x_n. \end{align*}\]

  4. The operation \(+\) on \(\mathbb{N}\) is a function \[\begin{align*} \mathbb{N} \times \mathbb{N} &\to \mathbb{N} \\ (a, b) &\mapsto a + b. \end{align*}\]

  5. A set \(X\) has size \(n\) iff there is a bijection \[\begin{align*} \{1, 2, \dots, n\} &\to X = \{a_1, \dots, a_n\} \\ i &\mapsto a_i \end{align*}\]

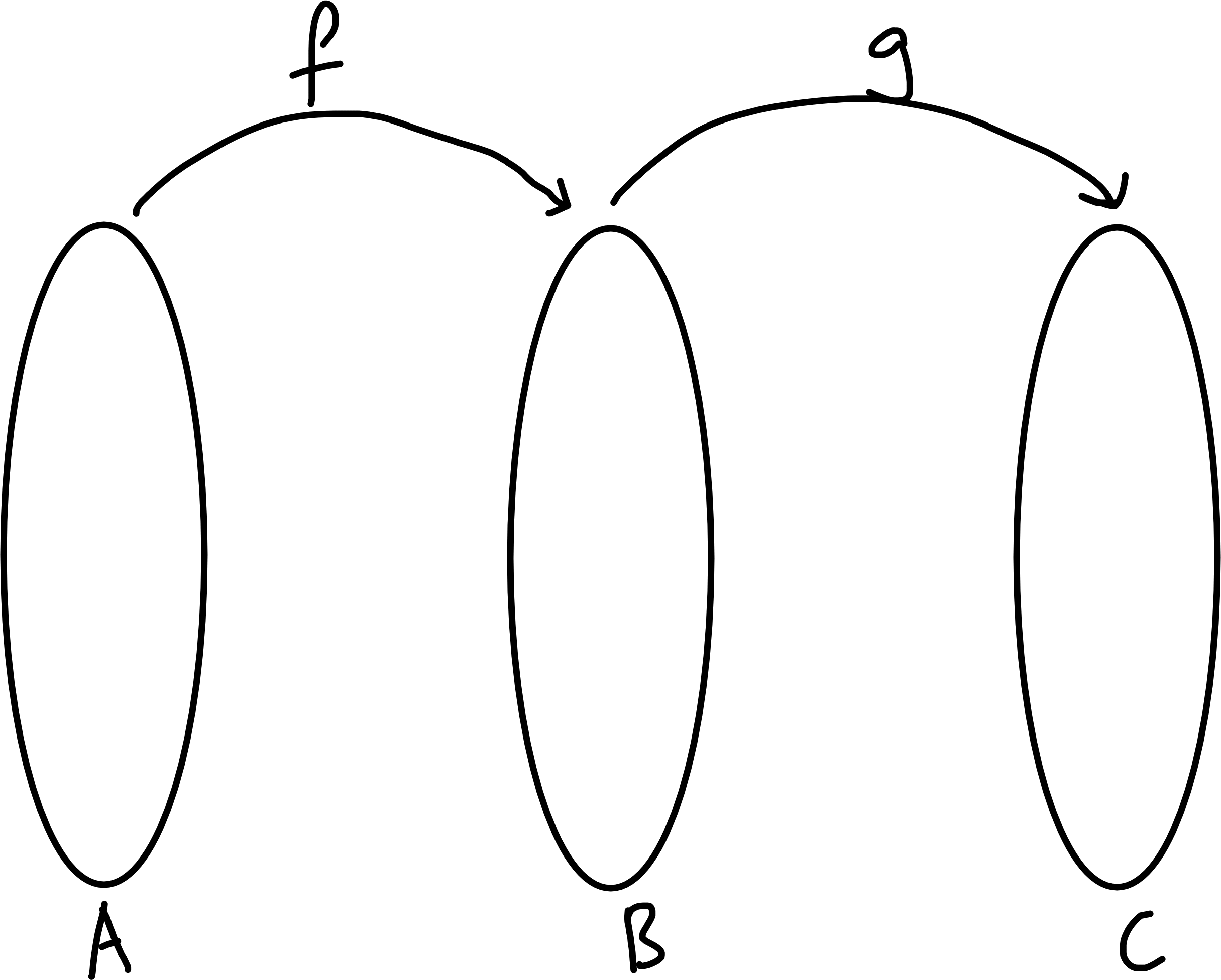
Definition 4.7 (Composition of functions) Given \(f : A \to B\) and \(g: B \to C\) the composition is \[\begin{align*} g \circ f : A &\to C \\ a &\mapsto g(f(a)). \end{align*}\] (“g composed with f”, “g circle f” or “g after f”).

Example 4.5 \[\begin{align*} \text{If } f : \mathbb{R} &\to \mathbb{R} & \text{ and } g : \mathbb{R} &\to \mathbb{R} \\ x &\mapsto 2x & x &\mapsto x + 1 \end{align*}\] then \(g \circ f(x) = g(f(x)) = g(2x) = 2x + 1\)
and \(f \circ g(x) = f(g(x)) = f(x + 1) = 2x + 2\).

So in general, \(\circ\) is not commutative.
In the example above, \(f \circ g \neq g \circ f\) since \(f \circ g(1) = 4 \neq 3 = g \circ f(1)\).

However, \(\circ\) is associative, i.e. given \(f: A \to B\), \(g: B \to C\), \(h: C \to D\), we have \(h \circ (g \circ f) = (h \circ g) \circ f\).

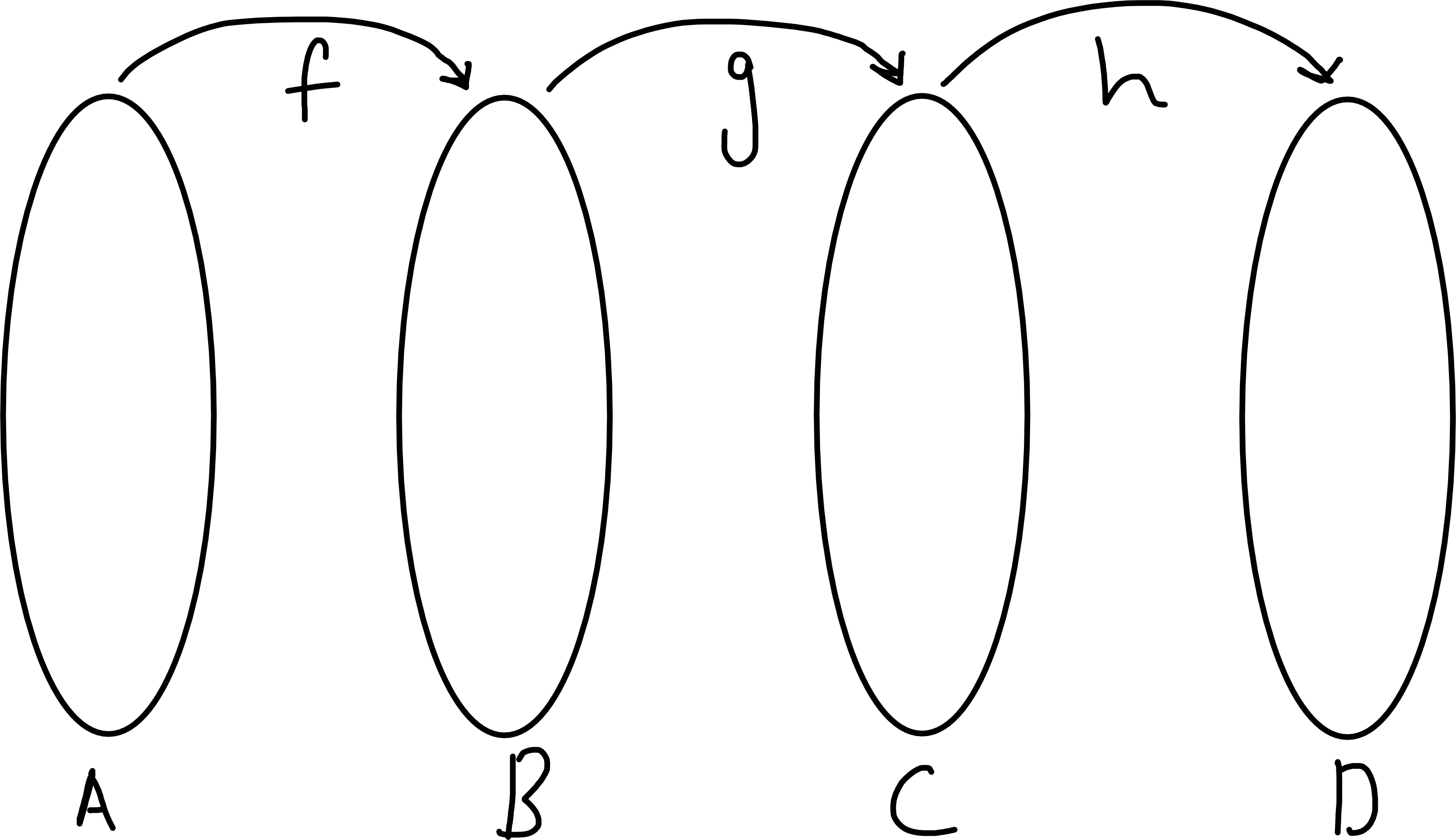
Proof. Indeed, for every \(x \in A\), \[\begin{align*} (h \circ (g \circ f))(x) &= h ((g \circ f)(x)) \\ &= h(g(f(x))) \\ \text{and } ((h \circ g) \circ f)(x) &= h \circ g(f(x)) \\ &= h(g(f(x))). \end{align*}\]

We may therefore drop the brackets and write \(h \circ g \circ f\) without ambiguity.

Definition 4.8 (Inverse function) We say \(f: A \to B\) is invertible if \(\exists \; g : B \to A\) s.t. \(g \circ f = \text{id}_A\) and \(f \circ g = \text{id}_B\).

Example 4.6 \[\begin{align*} f : \mathbb{R} &\to \mathbb{R} & g : \mathbb{R} &\to \mathbb{R} \\ x &\mapsto 2x + 1 & x &\mapsto \frac{x - 1}{2}. \end{align*}\] Indeed, \(\forall \; x \in \mathbb{R}, (g \circ f)(x) = g(2x + 1) = \frac{2x + 1 - 1}{2} = x\) so \(g \circ f = \text{id}_\mathbb{R}\).
Also \(\forall \; x \in \mathbb{R}, (f \circ g)(x) = f\left(\frac{x - 1}{2}\right) = 2 \frac{x - 1}{2} + 1 = x\) so \(f \circ g = \text{id}_\mathbb{R}\). Hence \(f\) is invertible with inverse \(g\).

Warning For example, \[\begin{align*} f : \mathbb{N} &\to \mathbb{N} & g : \mathbb{N} &\to \mathbb{N} \\ x &\mapsto x + 1 & x &\mapsto \begin{cases} x - 1 & \text{if } x \neq 1 \\ 1 & \text{if } x = 1 \end{cases} \end{align*}\] have \(g \circ f = \text{id}_\mathbb{N}\) but \(f \circ g \neq \text{id}_\mathbb{N}\) because \(f \circ g(1) \neq 1\).

Given \(f: A \to B\), when is there a map \(g : B \to A\) s.t. \(g \circ f = \text{id}_A\)?
If such a \(g\) exists, and \(a, a' \in A\) are s.t. \(f(a) = f(a')\), then \(gf(a) = gf(a')\) so \(a = a'\). Therefore \(f\) must be injective.
Conversely, if \(f\) is injective, we can find \(g\) s.t. \(g \circ f = \text{id}_A\): if \(b \in f(A)\), let \(g(b) = a\), where \(a\) is the unique element of \(A\) with \(f(a) = b\); if \(b \notin f(A)\), let \(g(b)\) be anything you like19.

Given \(f : A \to B\), when is there a map \(g : B \to A\) s.t. \(f \circ g = \text{id}_B\)?
\(f \circ g = \text{id}_B \implies f(g(b)) = b \quad \forall \; b \in B\) so we need \(f(g(B)) = B\), so \(f\) must be surjective.
Conversely, if \(f\) is surjective, we can find \(g: B \to A\) with \(f \circ g = \text{id}_B\): for each \(b \in B\), pick some \(a \in A\) with \(f(a) = b\) and put \(g(b) = a\).

It follows that \(f : A \to B\) is invertible iff \(f\) is bijective. We write \(f^{-1} : B \to A\) for the inverse of \(f\) when it exists.

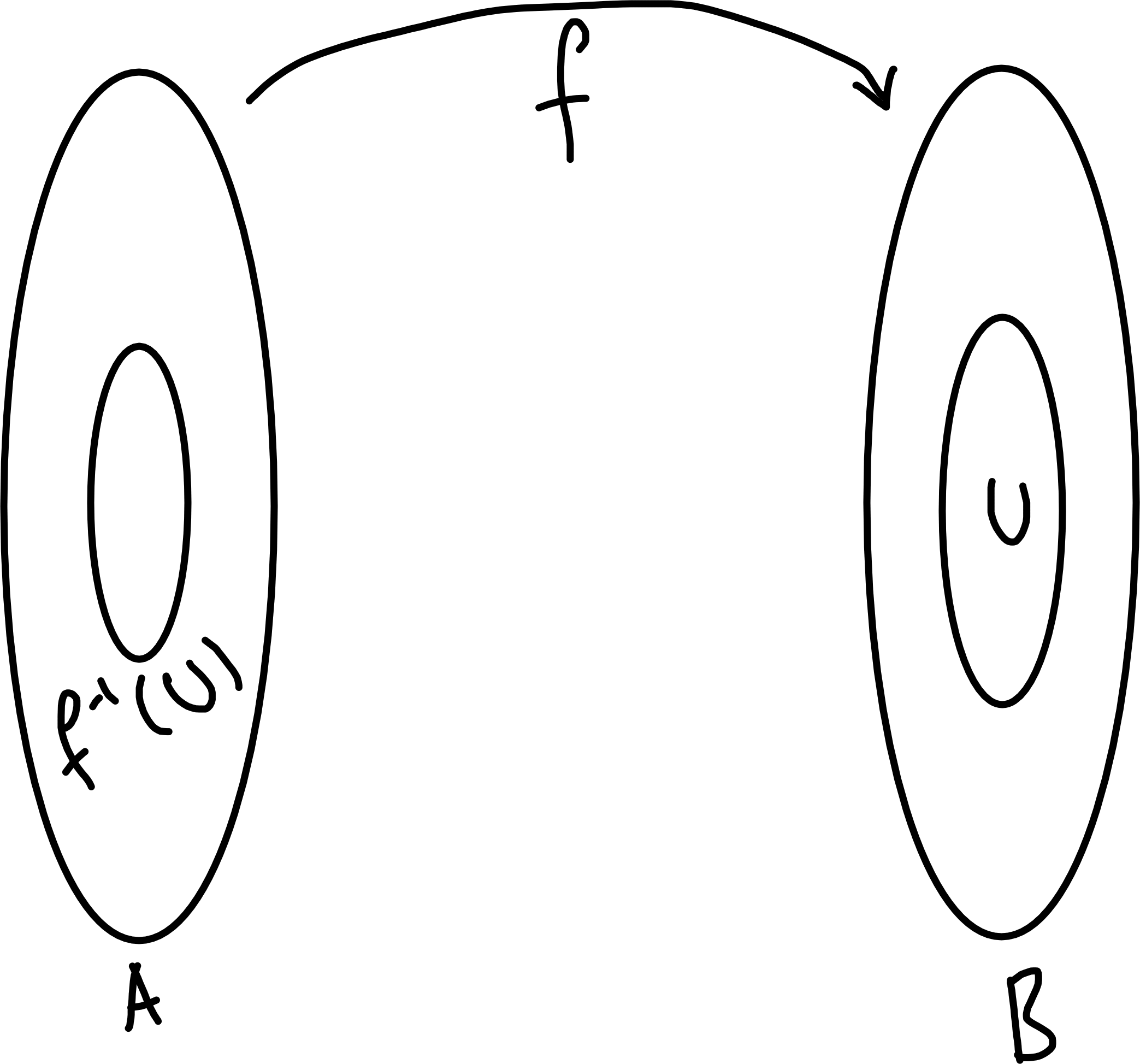
Note: Given \(f : A \to B\) and \(U \subseteq B\), we sometime write \(f^{-1}(U) = \{a \in A : f(a) \in U\}\) for the preimage of \(U\). This does not mean that \(f\) has an inverse!

4.3 Relations

A relation on a set \(X\) is a subset \(R \subseteq X \times X\). We usually write \(aRb\) (“\(a\) is related to \(b\)”) for \((a, b) \in R\).

Example 4.7 (Relations on ℕ)

  1. \(aRb\) if \(a, b\) have the same final digit;
  2. \(aRb\) if \(a \mid b\);
  3. \(aRb\) if \(a \neq b\);
  4. \(aRb\) if \(a = b = 1\);
  5. \(aRb\) if \(|a - b| \leq 3\);
  6. \(aRb\) if either \(a, b \leq 4\) or \(a, b \geq 5\).

There are three properties that a relation might have that are of special interest.

Definition 4.9 (Reflexive relation) \(R\) is reflexive if \(\forall \; x \in X,\ xRx\).

Definition 4.10 (Symmetric relation) \(R\) is symmetric if \(\forall \; x, y,\ xRy \implies yRx\) (swapping \(x, y\) gives \(\iff\)).

Definition 4.11 (Transitive relation) \(R\) is transitive if \(\forall \; x, y, z \in X,\ xRy\) and \(yRz \implies xRz\).

Example 4.8 With regards to the examples above, \[\begin{array}{lcccccc} \hline \text{Examples } & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline \text{Reflexive } & \checkmark & \checkmark & \times & \times & \checkmark & \checkmark \\ \text{Symmetric } & \checkmark & \times & \checkmark & \checkmark & \checkmark & \checkmark \\ \text{Transitive } & \checkmark & \checkmark & \times & \checkmark & \times & \checkmark \\ \hline \end{array}\]

Definition 4.12 (Equivalence relation) A relation \(R\) is an equivalence relation if it is reflexive, symmetric and transitive. We often write \(a \sim b\) for \(aRb\).

So (1) and (6) are equivalence relations. We have already seen another one:
(7). \(X = \mathbb{Z}\) with \(a \sim b\) if \(a \equiv b \mod 5\). This equivalence relation partitions \(\mathbb{Z}\) into “pieces” consisting of related elements, namely \(\{x \in \mathbb{Z} : x \equiv 0 \mod 5\}, \{x \in \mathbb{Z} : x \equiv 1 \mod 5\}, \dots, \{x \in \mathbb{Z} : x \equiv 4 \mod 5\}\).

Definition 4.13 (Partition of set) Given a set \(X\), a partition of \(X\) is a collection of pairwise disjoint subsets (called “parts”) whose union is \(X\).

Definition 4.14 (Equivalence class) If \(\sim\) is an equivalence relation on \(X\), then the equivalence class of \(x \in X\) is \[\begin{align*} [x] = \{y \in X : y \sim x\}. \end{align*}\]

E.g. in (1), \([376] = \{\)all natural numbers ending in \(6\}\).
in (7), \([12] = \{y : y \equiv 2 \mod 5\}\).

Important observation Given a partition of \(X\), there is an equivalence relation \(R\) whose equivalence classes are precisely the parts of the partition: just define \(a \sim b\) if \(a\) and \(b\) lie in the same part.

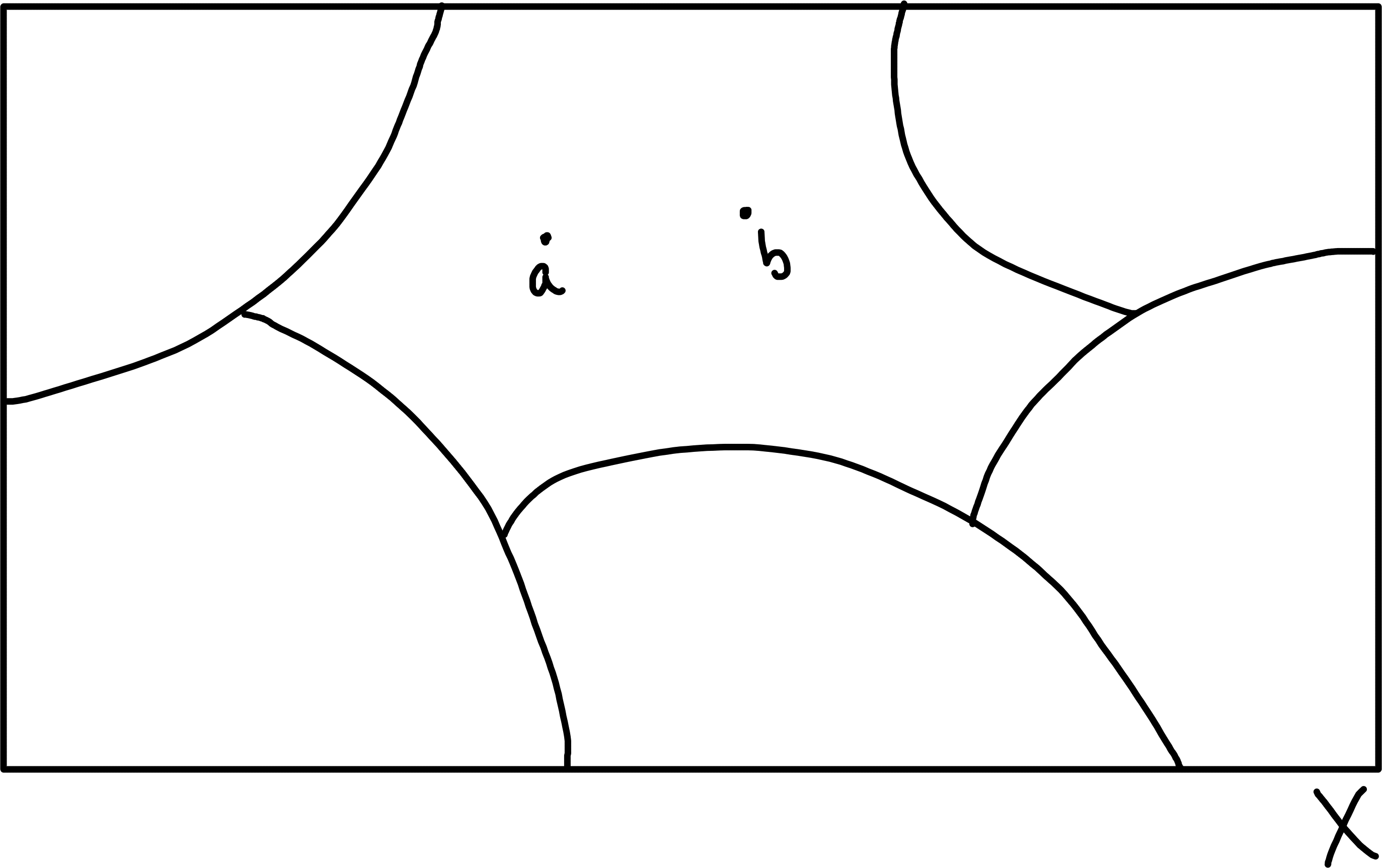
Theorem 4.3 Let \(\sim\) be any equivalence relation on \(X\). Then the equivalences classes form a partition of \(X\).

Proof. Since \(\sim\) is reflexive, we have \(x \in [x] \; \forall \; x \in X\). Thus \(\bigcup_{x \in X} [x] = X\). It remains to show that \(\forall \; x, y \in X\), either \([x] \cap [y] = \emptyset\) or \([x] = [y]\). Suppose \([x] \cap [y] \neq \emptyset\), and let \(z \in [x] \cap [y]\).
Then \(z \sim x\), so by symmetry \(x \sim z\), and \(z \sim y\). Then by transitivity, \(x \sim y\). Let \(w \in [y]\), so \(y \sim w\). Since \(x \sim y\) and \(y \sim w\) by transitivity, \(x \sim w\). Thus \(w \in [x]\).
Hence if \([x] \cap [y] \neq \emptyset\), then \([y] \subseteq [x]\); similarly, \([x] \subseteq [y]\). So \([x] = [y]\)

This is a useful viewpoint: it is not easy to see that there is an equivalence relation on \(\mathbb{N}\) with \(3\) equivalence classes, of which \(2\) are infinite and \(1\) is finite - simply take a partition of \(\mathbb{N}\) with this property.

Definition 4.15 (Quotient) Given an equivalence relations \(R\) on a set \(X\), the quotient of \(X\) by \(R\) is \[\begin{align*} X / R = \{ [x] : x \in X\} \end{align*}\]

E.g. in (7), \(X / R\) has size \(5\), in (1) has size \(10\). In fact, this explains why we sometimes write \(\mathbb{Z} / 5 \mathbb{Z}\) (the relation is whether two integers if their difference is a multiple of 5) instead of \(\mathbb{Z}_5\).

Definition 4.16 (Quotient map) The map \[\begin{align*} q : X &\to X / R \\ x &\mapsto [x] \end{align*}\] is the quotient map (or projection map).

Example 4.9 On \(\mathbb{Z} \times \mathbb{N}\), define \((a, b) R (c, d)\) if \(ad = bc\). It is easy to see that is an equivalence relation.
E.g. \([(1, 2)] = \{(1, 2), (2, 4), (3, 6) \dots \}\) so we can regard \(\mathbb{Z} \times \mathbb{N} / R\) as a copy of \(\mathbb{Q}\) by identifying \([(a, b)]\) with \(\frac{a}{b} \in \mathbb{Q}\). The quotient map \[\begin{align*} q : \mathbb{Z} \times \mathbb{N} &\to \mathbb{Z} \times \mathbb{N} / R \\ (a, b) &\to \frac{a}{b}. \end{align*}\]

  1. This justifies why we need the notion of the empty set, otherwise we wouldn’t be able to take the intersection of arbitrary pairs of sets.↩︎

  2. Note we can define \((a, b) = \{a, \{a, b\}\}\), the first element and the unordered pair.↩︎

  3. We do this so we have a size \(0\) set↩︎

  4. we use \(\mapsto\) for the assignment of individual elements↩︎

  5. as \(g \circ f\) will never lead to \(g(b)\) if \(b \notin f(A)\)↩︎