2 Elementary Number Theory

2.1 The natural numbers

Intuitively, the natural numbers consist of $1, 1 + 1, 1+ 1 + 1, \dots$

How do you know you have captured all natural numbers? How do you know they are all distinct?

We shall assume:

Definition 2.1 (Peano Axioms) The natural numbers, $\mathbb{N}$, is a set containing a special element ‘$1$’ with an operation ‘$+1$’ satisfying

$\forall \; n \in \mathbb{N},\ n + 1 \neq 1$;
$\forall \; m, n \in \mathbb{N},\ \text{ if } m \neq n,\ \text{ then } m + 1 \neq n + 1$
for any property $P(n)$, if $P(1)$ is true and $\forall \; n \in \mathbb{N}, P(n) \implies P(n + 1),$ then $P(n)$ is true for all natural numbers

iii is called the induction axiom.

i and ii capture the idea that any two natural numbers are distinct; iii captures our intuitive notion that the list⁵ is complete (i.e. encompasses all natural numbers).⁶

Now we can write 2 for $1 + 1$, 3 for $1 + 1 + 1$, etc, and we can define an operation ‘$+ k$’ for any natural number $k$:

$\hspace{1cm}$ for every natural number $n$, we know $n + (k + 1) = (n + k) + 1$;

$\hspace{1cm}$ and so by induction, taking $P(k)$ = “‘$+k$’ is defined”, proved.

Similarly, we can define multiplication, powers, etc. You may check that the “normal” rules of arithmetic apply:

\[\begin{align} &1.\ \forall \; a, b, \in \mathbb{N} & &a + b = b + a & &(+ \text{ is commutative}); \\ &2.\ \forall \; a, b, \in \mathbb{N} & &ab = ba & &(\times \text{ is commutative}); \\ &3.\ \forall \; a, b, c \in \mathbb{N} & &a + (b + c) = (a + b) + c & &(+ \text{ is associative}); \\ &4.\ \forall \; a, b, c \in \mathbb{N} & &a (b c) = (a b) c & &(\times \text{ is associative}); \\ &5.\ \forall \; a, b, c \in \mathbb{N} & &a (b + c) = ab + ac & &(\times \text{ is distributive over }+); \end{align}\]

We can define $a < b$ if $a + c = b$ for some $c \in \mathbb{N}$. You may want to check

\[\begin{align} &6.\ \forall \; a, b, c & a < b &\implies a + c < b + c \\ &7.\ \forall \; a, b, c & a < b &\implies a c < b c \\ &8.\ \forall \; a, b, c & a < b \text{ and } b < c &\implies a < c \\ &9.\ \forall \; a & &\lnot (a < a). \end{align}\]

Recall the induction axiom: if $P(1)$ holds and $\forall \; n \in \mathbb{N}, P(n) \implies P(n+1)$, then $P(n)$ holds $\forall \; n \in \mathbb{N}$. This is also known as the (weak) principle of induction (WPI). A more useful form is the Strong Principle of Induction (SPI): if

$P(1)$ holds and
$\forall \; n \in \mathbb{N}$, we have $P(m) \;\forall \; m \leq n \implies P(n + 1)$,

then $P(n)$ holds $\forall \; n \in \mathbb{N}$.

In fact, WPI and SPI are equivalent. SPI $\implies$ WPI should be fairly clear. To see WPI $\implies$ SPI, apply the former to $Q(n) = `P(m) \; \forall \; m \leq n'$

Well-ordering Principle (WOP): If $P(n)$ holds for some $n \in \mathbb{N}$, then there is a least $n \in \mathbb{N}$ s.t. $P(n)$ holds. An alternative phrasing is “every non-empty subset of $\mathbb{N}$ has a minimal element”.

Theorem 2.1 SPI is equivalent to the WOP.

Proof. To show that WOP implies SPI, we assume 1 and 2 from SPI, and show that $P(n)$ holds $\forall \; n \in \mathbb{N}$ using WOP.

Suppose, on the contrary, that $P(n)$ is not true $\forall \; n \in \mathbb{N}$. Then $C = \{n \in \mathbb{N}: P(n) \text{ is false}\} \neq \emptyset$. By WOP, $C$ has a minimal element, $m$. Now $\forall \; k < m$, $k \notin C$ (by minimality of $m$), so $P(k)$ holds $\forall \; k < m$. But by 2 of SPI, $P(m)$ holds, so contradicting $m \in C$. Hence SPI holds.

To show that SPI implies WOP, suppose there is no least $n \in \mathbb{N}$ s.t. $P(n)$ holds. We want to show that $P(n)$ does not hold for any $n \in \mathbb{N}$, using SPI.

Consider $Q(n) = `\lnot P(n)'$. Certainly $P(1)$ is false (else $1$ would be the minimal element), so $Q(1)$ holds.

Given $n \in \mathbb{N}$, suppose that $Q(k)$ is true $\forall \; k < n$. Then $P(k)$ is false $\forall \; k < n$. So $P(n)$ is false as otherwise $n$ would be the minimal element for which $P$ holds. Hence $Q(n)$ is true, and 2 of SPI holds, so $Q(n)$ is true $\forall \; n \in \mathbb{N}$. Thus $P(n)$ is false $\forall \; n \in \mathbb{N}$.

WOP enables us to prove $P(n)$ is true $\forall \; n \in \mathbb{N}$ as follows: If not, then there is a minimal counterexample, and we try and derive a contradiction.

2.2 The integers

The integers, written $\mathbb{Z}$, consist of all symbols $n, -n$, where $n \in \mathbb{N}$, and $0$.

We can define $+$ and $\times$ etc on $\mathbb{Z}$ using $\mathbb{N}$, and check that the usual rules of arithmetic hold. We also have \[\begin{align*} &10.\ \forall \; a \in \mathbb{Z} & a + 0 &= a & &(\text{identity for } +) \\ &11.\ \forall \; a \in \mathbb{Z}, & \exists \; b \in \mathbb{Z} \text{ s.t. } a + b &= 0 & &(\text{inverses for } + ) \end{align*}\]

Define ‘$a < b$’ if $a + c = b$ for some $c \in \mathbb{N}$. Rules 6, 8, 9 continue to hold, but 7 must be modified

7’. $\forall \; a, b, c \in \mathbb{Z}, a < b \text{ and } c > 0 \implies ac < bc.$

2.3 The rationals

The rationals, written $\mathbb{Q}$, consist of all expressions $\frac{a}{b}$ (note this is not division as we have not defined division, it just looks the same), where $a, b \in \mathbb{Z}$, $b \neq 0$, and $\frac{a}{b}$ and $\frac{c}{d}$ are regarded as the same if $ad = bc$.

Define $\frac{a}{b} + \frac{c}{d} = \frac{ad + bc}{bd}$, and check it does not matter how we wrote $\frac{a}{b}$ or $\frac{c}{d}$.

We similarly define multiplication, and $`\frac{a}{b} < \frac{c}{d}'$ where $b, d > 0$ if $ad < bc$. You can check all preceding rules apply.

In addition \[\begin{align*} 12.\ \forall \; a \in \mathbb{Q},\ a \neq 0,\ \exists \; b \ \text{ s.t. } ab &= 1 & &(\text{inverses for } \times) \end{align*}\]

Note. $\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q}$.

2.4 Primes

Given $a, b \in \mathbb{Z}$ we say “$a$ divides $b$” if $\exists \; c \in \mathbb{Z}$ s.t. $b = ac$. We might also say “$a$ is a divisor/ factor of $b$” or “$b$ is a multiple of $a$”. We write $a \mid b$ for $a$ divides $b$.

For any $b \in \mathbb{Z}$, $\pm 1$ and $\pm b$ are always factors; all others are called proper.

A natural number $n \geq 2$ is prime if its only factors are $\pm 1$ and $\pm n$.⁷ If $n \geq 2$ is not prime, then it is composite.

Proposition 2.1 Every natural number $n \geq 2$ can be written as a product of primes.

Proof. By induction on $n$. True for $n = 2$. Let $n > 2$ and suppose that the claim holds up to and including $n - 1$ (SPI). If $n$ is a prime, we are done. If $n$ is composite, then $n = a b$ for some $1 < a, b < n$. By the induction hypothesis, have $a = p_1 \dots p_k$, $b = q_1 \dots q_l$ for some primes $p_1 \dots p_k, q_1 \dots q_l$. Hence $n = ab = p_1 \dots p_k q_1 \dots q_l$ is a product of primes.

Theorem 2.2 There are infinitely many primes.

Proof (Euclid 300 BC). Suppose there are finitely many primes, say $p_1, \dots, p_k$. Let $N = p_1 \dots p_k + 1$. Then $p_1 \nmid N$, else $p_1 \mid (N - p_1 \dots p_k) = 1$. Clearly $p_1 \mid 1$ is false. Likewise, none of $p_2, p_3 \dots, p_k$ divide $N$, contradicting the fact that $N$ can be written as a product of primes.

Can a number have more than one factorisation in its primes? Our proof of 2.1 does not give uniqueness.

Clearly, $21 = 3 \cdot 7$ is unique. Why is $9049 \cdot 40099 \neq 6701 \cdot 54151$?

We shall need:

Proposition 2.2 If $p$ is a prime and $p \mid ab$ then $p \mid a$ or $p \mid b$.

Proof is later on, just below 2.1.

2.5 Highest Common Factors

Definition 2.2 Given $a, b \in \mathbb{N}$, a natural number $c$ is the highest common factor (hcf), or greatest common divisor (gcd) of $a$ and $b$ if

$c \mid a$ and $c \mid b$ “c is a common divisor of $a$ and $b$”
$d \mid a$ and $d \mid b \implies d \mid c$ “every common factor of $a$ and $b$ divides $c$”

We write $c = \operatorname{hcf}(a, b)$ or $c = \operatorname{gcd}(a, b)$, or simply $c = (a, b)$ \[\begin{align*} \text{E.g. the factors of } &12 \text{ are } 1, 2, 3, 4, 6, 12 \\ &18 \ \phantom{are} \ 1, 2, 3, 6, 9, 18 \end{align*}\] So the common factors are $1, 2, 3, 6$, hence $\operatorname{hcf}(12, 18) = 6$. But if $a$ and $b$ had common factors $1, 2, 3, 4, 6$ then $a$ and $b$ would have no $\operatorname{hcf}$ (according to ii). Therefore, we will need to show that $\operatorname{hcf}(a, b)$ always exists.

Proposition 2.3 (Division Algorithm) Let $n, k \in \mathbb{N}$. Then we can write $n = qk + r$, where $q$ and $r$ are integers with $0 \leq r \leq k - 1$.

Proof. By induction on $n$. True for $n = 1$.

Suppose $n - 1 = q k + r$ for some $q, r \in \mathbb{Z}$, $0 \leq r \leq k - 1$.

If $r < k - 1$ then $n = (n - 1) + 1 = qk + (r + 1)$.

If $r = k - 1$ then $n = (n - 1) + 1 = qk + (k - 1) + 1 = (q + 1)k$.

2.6 Euclid’s Algorithm

\[\begin{array}{c|cc|c} \text{INPUT} & a & b & a = 372,\ b = 162 \\ \hline \text{STEP } 1& a = q_1 b + r_1 & q_1, r_1 \in \mathbb{Z} & 372 = 2 \cdot 162 + 48 \\ & & 0 \leq r \leq b - 1 & \\ \text{STEP } 2& b = q_2 r_1 + r_2 & 0 \leq r_2 < r_1 & 162 = 3 \cdot 48 + 18 \\ \text{STEP } 3& r_1 = q_3 r_2 + r_3 & 0 < r_3 < r_2 & 48 = 2 \cdot 18 + 12 \\ \vdots & \vdots & \vdots & \vdots \\ \text{STEP } n& r_{n - 2} = q_n r_{n-1} + r_{n} & 0 \leq r_n < r_{n - 1} & 18 = 1 \cdot 12 + 6 \\ \text{STEP } n + 1& r_{n - 1} = q_{n + 1} r_n + r_{n + 1} & r_{n + 1} = 0 & 12 = 2 \cdot 6 & \\ \hline \text{OUTPUT} & r_n &&& \end{array}\]

Note that the algorithm terminates in $\leq b$ steps, since $b > r_1 > r_2 > \dots \geq 0$.

Theorem 2.3 The output of Euclid’s algorithm with input $a, b$ is $\operatorname{hcf}(a, b)$.

Proof.

\[\begin{align*} \text{We can see } &r_n \mid r_{n - 1} \text{ (as } r_{n + 1} = 0 \text{ at STEP } n + 1 \text{)} \\ \text{so } &r_n \mid r_{n - 2} \ ( \text{STEP } n) \\ \text{so } &r_n \mid r_i \quad \forall \; i = 1, \dots n - 1 \text{ (by induction)} \end{align*}\] Hence $r_n \mid b$ (STEP $2$) and $r_n \mid a$ (STEP $1$).
Given $d$ s.t. $d \mid a$ and $d \mid b$, \[\begin{align*} \text{we have } &d \mid r_1 \text{ (STEP 1) } \\ \text{so } &d \mid r_2 \text{ (STEP 1) } \\ \text{so } &d \mid r_i \; \forall \; i = 1, \dots n \text{ (by induction)} \end{align*}\] Therefore, $r_n = \operatorname{hcf}(a, b)$.

Example 2.1 To obtain $\operatorname{hcf}(87, 52)$ we run Euclid: \[\begin{align*} 87 &= 1(52) + 35 \\ 52 &= 1(35) + 17 \\ 35 &= 2(17) + 1 \\ 17 &= 17(1) \end{align*}\] so $\operatorname{hcf}(87, 52) = 1$.

When $\operatorname{hcf}(87, 52) = 1$, we also say that $a$ and $b$ are coprime. We can reverse the algorithm: \[\begin{align*} 1 &= 35 - 2 * 17 \\ &= 35 - 2*(52 - 1(35)) \\ &= - 2(52) + 3(35) \\ &= - 2(52) + 3(87 - 1(52)) \\ &= -5(52) + 3(87) \end{align*}\]

Theorem 2.4 $\forall \; a, b \in \mathbb{N},\ \exists \; x,y \in \mathbb{Z}$ s.t. $xa + yb = \operatorname{hcf}(a, b)$. “We can write $\operatorname{hcf}(a, b)$ as a linear combination of $a$ and $b$.”

Proof (1). Run Euclid’s algorithm with input $a$, $b$, to obtain an output $r_n$. At STEP $n$, we have $r_n = xr_{n-1} + yr_{n-2}$ for some $x, y \in \mathbb{Z}$. But $r_{n-1}$ is expressible as $xr_{n-2} + yr_{n-3}$ for some $x, y \in \mathbb{Z}$, from STEP $n-1$, whence $r_n = xr_{n-2} + y r_{n-3}$ for some $x, y \in \mathbb{Z}$. Continuing by induction, we have that $\forall \; i = 2, \dots, n-1$, $r_n = xr_i + yr_{i - 1}$ for some $x, y \in \mathbb{Z}$. Thus $r_n = xa + yb$ for some $x, y \in \mathbb{Z}$, from STEP 1 and 2.

Remark. Euclid’s algorithm not only proves that $x, y \in \mathbb{Z}$, but it gives us a quick way to find them.

Proof (2). Let $h$ be the least positive combination of $a$ and $b$, i.e. the least positive integer of the form $xa + yb$ for some $x, y \in \mathbb{Z}$.

We shall show that $h = \operatorname{hcf}(a, b)$.

To see (ii) from 2.2, observe that a given $d$ s.t. $d \mid a$ and $d \mid b$, then we have $d \mid ax + by \; \forall \; x, y \in \mathbb{Z}$, so in particular $d \mid h$.

To verify (i), suppose that $h \nmid a$. Then we can write $a = qh + r$ for some $q, r \in \mathbb{Z}$ with $0 < r < h$⁸. Hence $r = a - qh = a - q(xa + yb)$, so $r$ is also a positive linear combination of $a$ and $b$, and strictly smaller than $h$, contradicting the definition of $h$. Therefore, $h \mid a$ and by the same argument, $h \mid b$.

Remark. Proof (2) tells us that $\operatorname{hcf}(a,b)$ exists and is a linear combination of $a$ and $b$, but gives no way to find $\operatorname{hcf}(a,b)$ or the coefficients $x, y$.

Is there an solution in integers $x, y$ to $320x + 72y = 33$. No, as LHS is always even but the RHS is odd.

What about $87x + 52y = 33$? Yes, as we had $x', y' \in \mathbb{Z}$ s.t. $87 x' + 52 y' = 1$, so $x = 33x'$, $y = 33y'$ is an integer solution.

Corollary 2.1 (Bezout's Theorem) Let $a, b \in \mathbb{N}$. Then the equation $ax + by = c$ has a solution in integers $x, y$ iff $\operatorname{hcf}(a, b) \mid c$.

Proof. Let $h = \operatorname{hcf}(a, b)$.

Suppose there are $x, y \in \mathbb{Z}$ s.t. $ax + by = c$. Then since $h \mid a$ and $h \mid b$, so $h \mid c$.

Conversely, suppose $h \mid c$. But Theorem 2.4 implies that there exist $x, y \in \mathbb{Z}$ s.t. $h = ax + by$. But then $c = \frac{c}{h} h = \frac{c}{h}(ax + by) = a(x \frac{c}{h}) + b(y \frac{c}{h})$.

We will now give a proof of proposition 2.2.

Proof. Suppose $p \mid ab$ but $p \nmid a$. We will show $p \mid b$. Then since $p$ is prime, $\operatorname{hcf}(a, p) = 1$ (as $p \nmid a$). Thus, by Theorem 2.4, $\exists \; x, y \in \mathbb{Z}$ s.t. $xp + ya = 1$.

It follows that $xpb + yab = b$, $p \mid ab$ so $p \mid b$.

Remark.

Similarly, $p \mid a_1 a_2 \dots a_n \implies p \mid a_i$ for some $i = 1, \dots, n$. Indeed, Proposition 2.2 tells us that if $p \mid a_1 a_2 \dots a_n$, then $p \mid a_1$ or $p \mid a_2 \dots a_n$. Proceed by induction on the number of terms in the product.
We do need $p$ to be prime.

Theorem 2.5 (Fundamental Theorem of Arithmetic) Every natural number $n \geq 2$ is expressible as a product of primes, uniquely up to reordering.

Proof. Existence of factorisation follows from Proposition 2.1. To see uniqueness, use induction on $n$. True for $n = 2$.

Given $n \geq 2$, suppose $n = p_1 p_2 \dots p_k = q_1 q_2 \dots q_l$, where $p_i, q_j$ are all prime. We want to show $k = l$ and, after reordering $p_i = q_i \; \forall \; i = 1, \dots, k$.

We have $p_1 \mid n = q_1 q_2 \dots q_l$, so by Proposition 2.2, $p_1 \mid q_i$ for some i. Relabelling the $q_i$, we may assume that $p_1 \mid q_1$. Since $q_1$ is prime, $p_1 = q_1$. So $\frac{n}{p_1} = p_2 \dots p_k = q_2 \dots q_l < n$.

By the induction hypothesis, $k = l$, and, after reordering, $p_2 = q_2, \dots, p_k = q_k$.

Remark. There are “arithmetical systems” (permitting addition, subtraction, multiplication) where factorisation is not unique.
For example, consider $\mathbb{Z}[\sqrt{-3}]$, meaning all complex numbers of the form $x + y \sqrt{-3} = x + y \sqrt{3}i$, where $x, y \in \mathbb{Z}$. We can add and multiply two elements of $\mathbb{Z}[\sqrt{-3}]$ to get another another element of $\mathbb{Z}[ \sqrt{-3}]$.
E.g. $(1 + \sqrt{-3}) \cdot (1 - \sqrt{-3}) = 1 + \sqrt{-3} - \sqrt{-3} + 3 = 4$.
In $Z[ \sqrt{-3} ]$, we can define what it means to be “prime”, and both $(1 + \sqrt{-3})$ and $(1 - \sqrt{-3})$ happen to be prime in this sense. But we can also write $4 = 2 \cdot 2$, so factorisation is not unique.

2.7 Some Applications of Theorem 2.5

What are the factors of $n = 2^3 \cdot 3^7 \cdot 11$?
All numbers of the form $2^a 3^b 11^c$, where $0 \leq a \leq 3,\ 0 \leq b \leq 7,\ 0 \leq c \leq 1$. There are no other factors, for example if $7 \mid n$ then we would have a factorisation of $n$ involving $7$, contradicting uniqueness.
More generally, the factors of $n = p_1^{a_1} \dots p_k^{a_k}$ are precisely the numbers of the form $p_1^{b_1} \dots p_k^{b_k}$, with $0 \leq b_i \leq a_i \; \forall \; i = 1, \dots, k$.
What are the common factors of $2^3 \cdot 3^7 \cdot 5 \cdot 11$ and $2^4 \cdot 3^2 \cdot 11 \cdot 13$?
All numbers of the form $2^a \cdot 3^b \cdot 5^c \cdot 11^d \cdot 13^e$, where $c = e = 0$ and $0 \leq a \leq 3,\ 0 \leq b \leq 2,\ 0 \leq d \leq 1$. Thus the hcf is $2^3 \cdot 3^2 \cdot 11$.

In general, the hcf of $p_1^{a_1} \dots p_k^{a_k}$ and $p_1^{b_1} \dots p_k^{b_k}$, where $a_i, b_i \geq 0$, is $p_1^{\min \{ a_1, b_1 \}} \dots p_k^{\min \{ a_k, b_k \}}$.
What are the common multiples of the two numbers in (2)? All numbers of the form $2^a 3^b 5^c 11^d 13^e$, where $a \geq 4, b \geq 7, c \geq 1, d \geq 3, e \geq 1$, times any integer!
Hence $2^4 3^7 5 11^3 13$ is a common multiple, and any other common multiple is a multiple of it. We say that it is the least common multiple (lcm) of our two numbers.

In general, the lcm of $p_1^{a_1} \dots p_k^{a_k}$ and $p_1^{b_1} \dots p_k^{b_k}$, where $a_i, b_i \geq 0$, is $p_1^{\max \{ a_1, b_1 \}} \dots p_k^{\max \{ a_k, b_k \}}$.

Since $\min \{ a_i, b_i \} + \max \{ a_i, b_i \} = a_i + b_i$, so we have $\operatorname{hcf}(x, y) \cdot \operatorname{lcm}(x, y) = x \cdot y$ for any $x, y$.
Another proof of Theorem 2.2, due to Erdos (1930):

Proof. let $p_1, \dots, p_k$ be primes. Any number which is a product of just these primes is of the form $p_1^{j_1} p_2^{j_2}, \dots p_k^{j_k} = m^2 p_1^{i_1} p_2^{i_2} \dots p_k^{i_k} (*)$ where $i_x = 0, 1$.
Let $M \in \mathbb{N}$. If a number $\leq M$ is of the form $(*)$, then $m^2 \leq M$, i.e. $m \leq \sqrt{M}$. So there are at most $\sqrt{M} 2^k$ of the form $(*)$ that are $\leq M$.
If $M > \sqrt{M} 2^k$, i.e $M > 4^k$, then there must be a number $\leq M$ which is not of the form $(*)$, which must have a prime factor not amongst $p_1, \dots, p_k$.

Proof 1 tells us the kth prime is $< 2^{2^k}$.
Proof 2 tells us kth prime is $< 4^k$.
In fact, we know kth prime $\sim k \log k$ (Prime Number Theorem).

2.8 Modular arithmetic

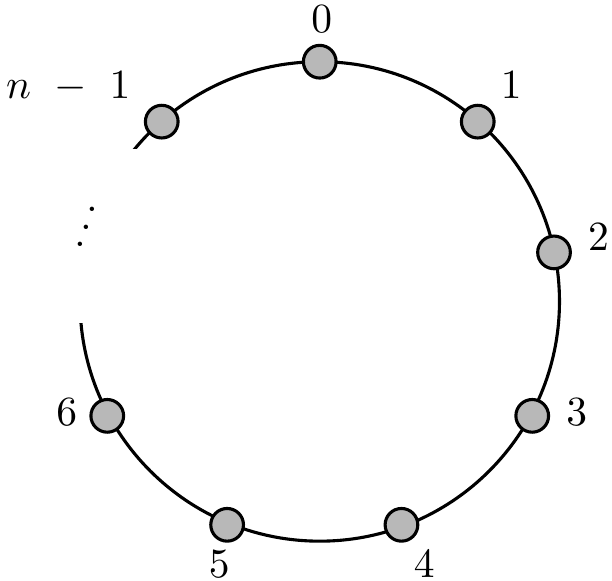
Let $n \geq 2$ be a natural number. Then the integers modulo n, written $\mathbb{Z}_n$ or $\mathbb{Z} / n \mathbb{Z}$, consist of the integers, with two regarded as the same if they differ by a multiple of $n$. E.g. In $\mathbb{Z}_7$, 2 is the same as 16. If $x$ and $y$ are the same in $\mathbb{Z}_n$, we write “$x \equiv y \mod n$” (is congruent to) or “$x \equiv y\ (n)$” or “$x = y \text{ in } \mathbb{Z}_n$”. E.g. $2 \equiv 16 \mod 7$ Thus \[\begin{align*} x \equiv y \mod n &\iff n \mid x - y \\ &\iff x = y + k n \text{ for some } k \in \mathbb{Z} \end{align*}\] We can view $\mathbb{Z}_n$ as

Note If $a \equiv a' \mod n$ and $b \equiv b' \mod n$, then $n \mid (a - a') + (b - b') = (a + b) - (a' + b')$ so $a + b \equiv a' + b' \mod n$.
Similarly, $n \mid (a - a') \cdot b + (b - b') \cdot a' = ab - a'b'$ so $ab \equiv a'b' \mod n$.
So we can do arithmetic modulo n.

Example 2.2 Does $2a^2 + 3b^3 = 1$ have a solution with $a, b \in \mathbb{Z}$?

Answer If there is a solution, then $2a^2 \equiv 1 \mod 3$, but $2 \cdot 0^2 \equiv 0$, $2 \cdot 1 ^2 \equiv 2$, $2 \cdot 2^2 \equiv 2 \mod 3$.

2.9 Solving congruences

Example 2.3 Solve $7x \equiv 2 \mod 10$. We note $3 \cdot 7 \equiv 1 \mod 10$, so $3 \cdot 7 x \equiv 3 \cdot 2 \mod 10$ so $x \equiv 6 \mod 10$.

Given $a, b \in \mathbb{Z}$, we say that b is an inverse of a modulo $n$ if $a b \equiv 1 \mod n$. We say $a$ is invertible modulo $n$, or is a unit modulo $n$, if it has an inverse. E.g. in $\mathbb{Z}_{10}$, the inverse of $3$ is $7$, and both $3$ and $7$ are units modulo $10$.
But $4$ is not a unit modulo $10$ since $4x \not\equiv 1 \mod 10 \; \forall \; x \in \mathbb{Z}$.

Remark. If $a$ is a unit modulo $n$ …

… its inverse is unique (mod $n$). Suppose $\exists \; b, b'$ s.t. $ab \equiv ab' \equiv 1 \mod n$, then $b \equiv bab \equiv bab' \equiv b' \mod n$.
… we can write $a^{-1}$ for its inverse.
… and $ab \equiv ac \mod n$, then $b \equiv c \mod n$. “We cancel units, multiplying both sides by $a^{-1}$.” This is not true in general: $4 \cdot 3 \equiv 4 \cdot 8 \mod 10$ but $3 \not\equiv 8 \mod 10$.

Proposition 2.4 Let $p$ be prime. Then every $a \not\equiv 0 \mod p$ is a unit modulo $p$.

Proof. Have $(a, p) = 1$⁹, so $\exists \; x, y \in \mathbb{Z}$ s.t. $ax + py = 1$. Hence $ax = 1 - py$, so $ax \equiv 1 \mod p$ for some $x \in \mathbb{Z}$.

Proposition 2.5 Let $n \geq 2$. Then $a$ is a unit modulo $n$ iff $(a, n) = 1$

Proof. \[\begin{align*} (a, n) = 1 &\iff ax + ny = 1 \text{ for some } x,y \in \mathbb{Z} \\ &\iff ax = 1 - ny \text{ for some } x,y \in \mathbb{Z} \\ &\iff ax \equiv 1 \mod n \text{ for some } x \in \mathbb{Z}. \end{align*}\]

Corollary 2.2 If $(a, n) = 1$, then the congruence $ax \equiv b \mod n$ has a unique solution (mod $n$). In particular, if $(a, n) = 1$, then there is a unique inverse of $a$, $a^{-1}$, modulo $n$. Both follow from previous remark.

What if $ax \equiv b \mod n$ with $(a, n) \neq 1$, say $(a, n) = d > 1$?
Then $n \mid ax - b$ so $d \mid ax - b$ and $d \mid a$, so if there is a solution, then $d \mid b$.
Conversely, if $d \mid b$, then $n = d \cdot n'$, $a = d \cdot a'$, $b = d \cdot b'$ and \[\begin{align*} ax \equiv b \mod n &\iff ax - b = kn \text{ for some } k \in \mathbb{Z} \\ &\iff d \cdot a' \cdot x - d \cdot b' = k \cdot d \cdot n' \text{ for some } k \in \mathbb{Z} \\ &\iff a' x - b' = k n' \text{ for some } k \in \mathbb{Z} \\ &\iff a'x \equiv b' \mod n'. \end{align*}\] Note $(a', b') = 1$.
So if $(a, n) = d > 1$, the congruence $ax \equiv b \mod n$ has no solutions unless $d \mid b$, in which case the solutions are exactly those of $\frac{a}{d}x \equiv \frac{b}{d} \mod \frac{n}{d}$.

Example 2.4 $7x \equiv 4 \pod {30}$.
We have $(7, 30) = 1$, so by Euclid $13 \cdot 7 - 3 \cdot 30 = 1$. Hence $13 \cdot 7 \equiv 1 \mod 30$, whence $x \equiv 4 \cdot 13 \mod 30 = 22 \mod 30$.

Suppose $x'$ is also a solution, that is $7x' \equiv 4 \mod 30$. Then $7x \equiv 7x' \mod 30$, so $x \equiv x' \mod 30$ since $7$ is a unit modulo $30$.

Short form: \[\begin{align*} 7x &\equiv 4 \mod 30 \\ \iff 13 \cdot 7 x &\equiv 13 \cdot 4 \mod 30 \quad \text{we have $\Longleftarrow$ since $13$ is a unit modulo $30$} \\ x &\equiv 22 \mod 30 \end{align*}\]

Example 2.5 $10x \equiv 12 \mod 34 \iff 10x = 12 + 34y$ \[\begin{align*} 10x \equiv 12 \mod 34 &\iff 10x = 12 + 34y \text{ for some } y \in \mathbb{Z} \\ &\iff 5x = 6 + 17y \text{ for some } y \in \mathbb{Z} \\ &\iff 5x \equiv 6 \mod 17 \end{align*}\] so now we’re back in situation 1, and solve this as before.

2.10 Solving simultaneous congruences

\[\begin{align*} \text{Note } x \equiv 5 \mod 12 \implies \begin{cases} x \equiv 1 \mod 4 \\ x \equiv 2 \mod 3 \end{cases}. \end{align*}\]

Is the converse true, i.e. does $x \equiv 1 \mod 4$ and $x \equiv 2 \mod 3$ imply $x \equiv 5 \mod 12$?
We inspect \[\begin{align*} x &\equiv 1 \mod 4,\ & x &\equiv 1, 5, 9 \mod 12 \\ x &\equiv 2 \mod 3,\ & x &\equiv 2, 5, 8, 11 \mod 12 \end{align*}\] What about \[\begin{align*} \begin{cases} x \equiv 1 \mod 4 \\ x \equiv 2 \mod 6 \end{cases}? \end{align*}\]

Theorem 2.6 (Chinese Remainder Theorem) Let $m, n$ be coprime, and $a, b \in \mathbb{Z}$. Then there is a unique solution modulo $mn$ to the simultaneous equations $x \equiv a \mod m$ and $x \equiv b \mod n$.
That is, there is a solution $x$ to $x \equiv a \mod m$ and $x \equiv b \mod n$, and y is a solution iff $x \equiv y \mod mn$.

Proof. Existence: Since $(m, n) = 1,\; \exists \; s, t \in \mathbb{Z}$ with $sm + tn = 1$.
Note $sm \equiv 1 \mod n$ as $tn \equiv 0 \mod n$ and $tn \equiv 1 \mod m$ as $sm \equiv 0 \mod m$.
Hence $x = a(tn) + b(sm) \equiv a \mod m \equiv b \mod n$.

Uniqueness: Suppose $y$ is also a solution, that is, $y \equiv a \mod m$ and $y \equiv b \mod n$. \[\begin{align*} &\;\;\; y \equiv a \mod m \text{ and } y \equiv b \mod n \\ &\iff y \equiv x \mod m \text{ and } y \equiv x \mod n \\ &\iff m \mid y - x \text { and } n \mid y - x \\ &\iff mn \mid y - x \hspace{0.5cm} \text{since } (m, n) = 1 \\ &\iff y \equiv x \mod mn \end{align*}\]

Remark. Theorem 2.6 can be extended by induction, to more than two moduli: if $m_1, m_2, \dots, m_k$ are pairwise coprime, then $\forall \; a_1, a_2, \dots, a_k \in \mathbb{Z},\ \exists\; x \in \mathbb{Z}$ s.t.\[\begin{align*} x &\equiv a_1 \mod m_1 \\ x &\equiv a_2 \mod m_2 \\ &\;\; \vdots \\ x &\equiv a_k \mod m_k \end{align*}\]

We denote by $\phi(m)$ the number of integers $a$ s.t. $1 \leq a \leq m$ s.t $(a, m) = 1$, that is, the number of units modulo $m$. We call $\phi$ the Euler totient function. Define $\phi(1) = 1$.
E.g. when $p$ is prime, $\phi(p) = p - 1$, and $\phi(p^2) = p^2 - p$ (there are $p$ multiples of $p$ that are $\leq p^2$).
When $p, q$ are distinct primes, $\phi(pq) = pq - p - q + 1$ (we subtracted $pq$ twice).

2.11 Fermat’s Little Theorem

How do powers of an integer behave modulo $p$?

Example 2.6 Modulo $7$, $2^1 \equiv 2$, $2^2 \equiv 4$, $2^3 \equiv 1$, $2^4 \equiv 2$ then repeat $4, 1, 2, 4, 1, 2, \dots$.
Modulo 11, $2^1 \equiv 2$, $2^2 \equiv 4$, $2^3 \equiv 8$, $2^4 \equiv 5$, $2^5 \equiv 10$, $2^6 \equiv 9$, $2^7 \equiv 7$, $2^8 \equiv 3$, $2^9 \equiv 6$, $2^{10} \equiv 1$ then repeat.

Theorem 2.7 (Fermat's Little Theorem) Let $p$ be a prime. Then $a^p \equiv a \mod p$ for all $a \in \mathbb{Z}$. Equivalently, $a^{p-1} \equiv 1 \mod p$ for all $a \not\equiv 0 \mod p$.

Multiply second statement by $a$ and check case of $a \equiv 0 \mod p$ to get first. $a \not\equiv 0 \mod p$ means $a$ is a unit modulo $p$ and so first statement gives second.

We are going to be a bit general in this proof so we can take the same arguments and apply to composite $p$.

Proof. If $a \not\equiv 0 \mod p$, then $a$ is a unit mod $p$.
Thus $ax \equiv ay \mod p$ iff $x \equiv y \mod p$ (multiply by a to go from right to left, and by $a^{-1}$ for converse). Hence the numbers $a, 2a, 3a, \dots, (p - 1)a$ are pairwise incongruent (distinct) modulo $p$ and $\not\equiv 0 \mod p$, so they are $1, 2, 3, \dots p - 1$ in some order.

Hence \[\begin{align*} a \cdot 2a \cdot 3a \cdot \dots \cdot (p - 1)a &\equiv 1 \cdot 2 \cdot 3 \dots \cdot (p - 1) \mod p \\ a^{p-1} (p - 1)! &\equiv (p - 1)! \mod p. \end{align*}\] But $(p - 1)!$ is a unit mod $p$ (since it is a product of units), so we can cancel it to obtain $a^{p-1} \equiv 1 \mod p$.

Theorem 2.8 (Fermat-Euler Theorem) Let $(a, m) = 1$. Then $a^{\phi(m)} \equiv 1 \mod m$ .

Proof. Let $U = \{ x \in \mathbb{N} : 0 < x < m : (x, m) = 1 \}$, be the set of units modulo $m$. Label the elements $u_1, u_2, \dots u_{\phi(m)}$. Then $a u_1, a u_2, \dots, a u_{\phi(m)}$ are all distinct and invertible modulo $m$ (since $a$ and $u_i$ are units), and hence they are $u_1, u_2, \dots u_{\phi(m)}$ in some order.

It follows that \[\begin{align*} a u_1 \cdot a u_2 \cdot \dots \cdot a u_{\phi(m)} &\equiv u_1 \cdot u_2 \cdot \dots u_{\phi(m)} \mod m, \end{align*}\] that is $a^{\phi(m)} z = z \mod m$ where $z = u_1 \cdot u_2 \cdot \dots u_{\phi(m)}$ is a product of units modulo $m$, therefore it itself is a unit. So we may cancel it to obtain $a^{\phi(m)} = 1 \mod m$

2.12 Results about primes

What is $(p - 1)!$ modulo $p$.

Example 2.7 \[\begin{align*} \text{Where } p &= 5,\ 4! = 24 \equiv -1 \mod 5 \\ p &= 7,\ 6! = 720 \equiv -1 \mod 7 \end{align*}\]

Lemma 2.1 Let $p$ be prime. Then $x^2 \equiv 1 \mod p \iff x \equiv \pm 1 \mod p$.

Note Modulo $8$, $1^2 = 3^2 = 5^2 = 7^2 = 1$. This make us think that $p$ being prime is important.

Proof. \[\begin{align*} x^2 \equiv 1 \mod p &\iff x^2 - 1 \equiv 0 \mod p \\ &\iff (x + 1) (x - 1) \equiv 0 \mod p \end{align*}\] Recall Proposition 2.2, if $p$ is prime and $p \mid a b$, then $p \mid a$ or $p \mid b$, so if $p$ is prime, then $ab \equiv 0 \mod p \iff a \equiv 0 \mod p$ or $b \equiv 0 \mod p$. Hence \[\begin{align*} x^2 \equiv 1 \mod p &\iff x + 1 \equiv 0 \mod p \text{ or } x - 1 \equiv 0 \mod p \\ &\iff x \equiv \pm 1 \mod p \end{align*}\]

Remark. More generally, a non-zero polynomial of degree $k$ over $\mathbb{Z}_p$ has at most k roots.

Theorem 2.9 (Wilson's Theorem) Let $p$ be prime. Then $(p - 1)! \equiv -1 \mod p$.

Proof. True for $p = 2$, so assume $p > 2$.
Note that the units modulo $p$ come in pairs whose product is $1$, together with some elements that are self-inverse, i.e. $x$ s.t. $x^2 \equiv 1 \mod p$.
But by lemma 2.1, the elements of $\mathbb{Z}_p$ that are self-inverse are $+ 1$ and $-1$, so the remaining $p - 3$ elements of $\mathbb{Z}_p$ come in inverse pairs. [E.g. when $p = 11$, $1, 10$ are self inverses and the pairs are $(2, 6),\ (3, 4),\ (5, 9),\ (7, 8)$].
Hence $(p - 1)!$ is the product of $\frac{p - 3}{2}$ pairs of inverses together with $+ 1$ and $- 1$, so $(p - 1)! \equiv -1 \mod p$.

When is $-1$ a square modulo $p$? (If ever.)

Example 2.8 When $p = 5, 2^2 \equiv 4 \equiv - 1 \mod 5$.
When $p = 7, 0^2 = 0, 1^2 = 1, 2^2 = 4, 3^2 = 2 \mod 7$ and we don’t need to check $4, 5, 6$ as $(-x)^2 = x^2$.
When $p = 13, 5^2 \equiv -1 \mod 13$.
No luck when $p = 19$.

Proposition 2.6 Let $p$ be an odd prime. Then $-1$ is a square modulo $p$ iff $p \equiv 1 \mod 4$.

Proof. Suppose $p \equiv 1 \mod 4$. By Wilson’s Theorem, 2.9, \[\begin{align*} -1 \equiv (p - 1)! &\equiv 1 \cdot 2 \cdot 3 \cdot \dots \cdot \frac{p - 1}{2} \cdot - \frac{p - 1}{2} \cdot \dots -3 \cdot -2 \cdot -1 \mod p \\ &\equiv (-1)^{\frac{p-1}{2}} \left( \left(\frac{p-1}{2} \right)! \right)^2 \mod p \end{align*}\] But if $p = 4k + 1$ for some $k \in \mathbb{Z}$, then \[\begin{align*} -1 \equiv (-1)^{2k} \left( (2k)! \right)^2 \mod p \end{align*}\] so $-1$ is a square mod $p$.

Suppose, on the other hand, that $p \equiv -1 \mod 4$, i.e. $p = 4k + 3$ for some $k \in \mathbb{Z}$. If $-1$ were a square mod $p$, i.e. if there were $z \in \mathbb{Z}$ s.t. $z^2 \equiv -1 \mod p$, then by Fermat’s little Theorem, 2.7, \[\begin{align*} 1 \equiv z^{p-1} \equiv z^{4k+2} \equiv z^{2(2k + 1)} &\equiv (-1)^{2k + 1} \mod p \\ &\equiv -1 \mod p, \end{align*}\] a contradiction.

Remark. When $p \equiv 1 \mod 4$, Wilson’s Theorem, 2.9, tells us a solution to $x^2 \equiv -1 \mod p$.
E.g. When $p = 29 = 4 \cdot 7 + 1$, $x = (2 \cdot 7)!$ works.

2.13 Public Key Cryptography

Let us agree to write messages as sequences of numbers, e.g. $A \to 00,\ B \to 1, \dots, Z \to 25, ! \to 26, \dots$ I wish for my IA students to be able to send me encrypted messages in such a way that I can decrypt them easily but the same in not true for any third-party observer. We use the

2.13.1 RSA Scheme (Rivest, Shamir, Adleman)

I think of two large primes $p, q$¹⁰. Let $n = pq$, and pick an encoding exponent $e$ coprime to $\phi(n) = (p - 1)(q - 1)$. I publish the pair $(n, e)$ (not the hcf).
To send me a message (i.e. a sequence of numbers), you chop it into pieces/ numbers $M < n$ and send me $M^e \mod n$, computed quickly by repeated squaring.

To decrypt, I work out $d$ s.t. $ed \equiv 1 \mod \phi(n)$ (by Euclid’s algorithm). Then I compute $(M^e)^d = M^{k \phi(n) + 1}$ for some $k \in \mathbb{Z}$ which is $\equiv M \mod n$ by Fermat-Euler, 2.8.

Note that in order to decrypt this message in this way, I needed $n$ and $d$, or $n, e$ and $\phi(n)$. Finding $\phi(n)$ is as hard as finding the prime factors of $n$, which is believed to be computationally hard.
It is not know if RSA can be broken without factorisation.

$1, 1 + 1, 1+ 1 + 1, \dots$↩︎
to see this rigorously, take $P(n)$ = “$n$ is on this list↩︎
We don’t allow $1$ to be a prime as we want to have unique prime factorisations and it would require every statement to say let $n$ be a prime not equal to $1$.↩︎
as $h \nmid a$↩︎
the hcf of $a$ and $p$ is 1↩︎
on the order of a hundred digits↩︎